Когда уравнение
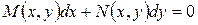 (1)
(1)
не является уравнением в полых дифференциалах, т.е. 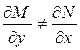 ,удается подобрать некоторую функцию
,удается подобрать некоторую функцию 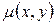 , такую что уравнение:
, такую что уравнение:
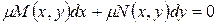 (2)
(2)
становится уравнением в полных дифференциалах. Общее решение полученного таким образом уравнения (2) совпадает с первоначальным решением уравнения (1). Функция 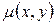 - наз. интегрирующим множителем уравнения (1).
- наз. интегрирующим множителем уравнения (1).
Для того, чтобы уравнение (2) было уравнением в полных дифференциалах необходимо и достаточно, чтобы выполнялось соотношение:
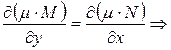
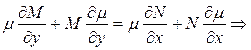
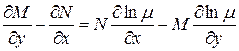 (3) - уравнение в частных производных 1-го порядка с неизвестной функцией
(3) - уравнение в частных производных 1-го порядка с неизвестной функцией 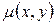 . Всякая функция удовлетворяющая уравнению (3) является интегрирующим множителем уравнения (1). Рассмотрим некоторые частные случаи, когда удаётся найти
. Всякая функция удовлетворяющая уравнению (3) является интегрирующим множителем уравнения (1). Рассмотрим некоторые частные случаи, когда удаётся найти 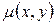 :
:
1) Случай интегрирующего множителя, зависящего только от 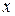 :
: 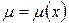 , тогда
, тогда 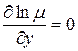 и из (3) следует:
и из (3) следует: 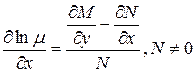 - обыкновенное дифференциальное уравнение, в котором
- обыкновенное дифференциальное уравнение, в котором 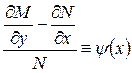 - функция от
- функция от 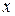 . В противном случае интегрирующего множителя вида
. В противном случае интегрирующего множителя вида 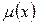 не существует.
не существует.
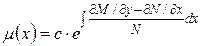
2) Случай интегрирующего множителя, зависящего только от 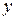 :
: 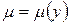 , тогда
, тогда 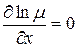 и из (3) следует
и из (3) следует 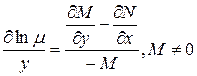 : - обыкновенное дифференциальное уравнение, в котором
: - обыкновенное дифференциальное уравнение, в котором 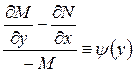 - функция от
- функция от 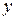 . В противном случае интегрирующего множителя вида
. В противном случае интегрирующего множителя вида 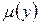 не существует.
не существует.
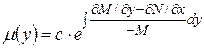
3) Случай интегрирующего множителя вида 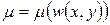 . Тогда
. Тогда
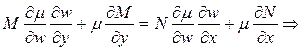
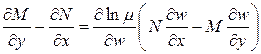 . Если
. Если 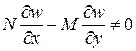 , то
, то 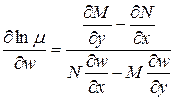 . Если
. Если 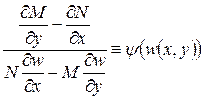 , то
, то 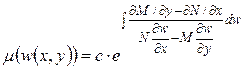 .
.
 2015-04-20
2015-04-20 2162
2162








