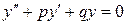Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Обобщение на случай уравнения n-ного порядка

(1)

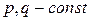
Для нахождения 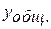достаточно найти два частных линейно независимых решени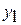й и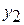

Эйлер предложил искать частные решения в виде 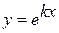, 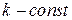(2)

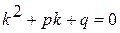(3) – характеристическое уравнение (1)

1 случай

корни характеристического уравнения действительны и различны

В этом случае частными решениями будут функции:

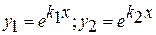
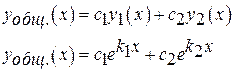
2 случай

корни характеристического уравнения комплексные

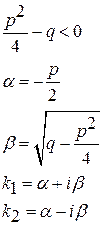
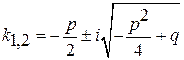
Частное решение:

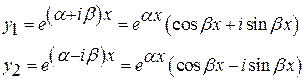
По теореме, действительная и мнимая части будут решениями, т.е. решениями будут действительные функции

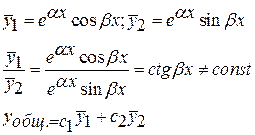
3 случай

корни характеристического уравнения действительны и равны

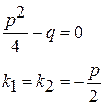
Одно частное решение получается 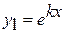. Второе частное решение независимое с первым будем искать в ви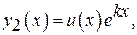де:

где 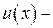неизвестная функция, подлежащая определению