F (x, y, y¢, y¢¢… y(n)) = 0 – обыкн. диф. уравнение. (1)
Иногда диф. ур. удается выразить произвольной высшей степени:
y(n) = f (x, y, y¢, y¢¢, …, y(n-1)) (2)
Для (1), (2) имеет место три осн-х задачи: задача Коши, краевая задача и задача на собственное знач-е.
Для диф. ур. (2) можно сформулировать теорему о существовании и единственности реш-я ур-я.
В частном случае (2) можно записать диф ур.-ем первого порядка: y¢= f (x, y) (3)
Теорема Коши: если функция f (x, y) и f¢у – непрерывны в области определения, то существует единственное решение у (х), удовлетворяющее начальному условию. у½х =х0 = у0 у (х0) = у. (4)
След.-но общее решение (3): у = j (х, с), (с – const)
Частное решение: у = j (х, с0).
Если обратиться к (2), то решение имеет вид
у = j (х, с1, с2, …, сп ), где const.-ы определяются из: 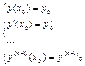 (5)
(5)
Для решения обыкн. диф. ур. как первого, так и высших порядков существует аналитич. методы, уже известные нам. Но при более сложных видах уравнений и нач. условий эти методы не позволяют дать решение. След.-но прибегают к числ. методам, для реализации кот. вводится понятие сетки. Отрезок [a,b], на кот. ищется решение, разбивается на n частичных с шагом h. Если h = const, т.е. сетка является равномерной, то
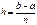 xk = x0 + k h (k = 1,2,..)
xk = x0 + k h (k = 1,2,..)
В основе числ. решения лежит идея замены диф. ур. его дискретным аналогом.
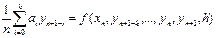 ( а0) ¹ 0 (6)
( а0) ¹ 0 (6)
Получение решения определяется по к предыдущим решениям. Этот метод наз. многошаговым. При к =1 – одношаговый
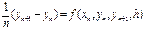 (7)
(7)
К одношаговым методам относ.: мет. Эйлера, видоизмен. мет. Эйлера, мет. Рунге-Кутта.
В (3) вместо независ. переменной х может быть t, следовательно, изучаются процессы, связанные со временем. Важной становится схема, по кот. реализуется решение (7):
1) явная схема: yn+1 = yn+ f (xn, yn) h (8)
2)неявная схема: yn+1 = yn+f (xn, yn, yn+1) h (9)
1)последнее решение ищется через предыдущее,
2) для нахождения последнего реш.-я надо решать систему нелинейных ур-й.
Выбор схемы влияет на скорость схождения решения и зависит от постановки задач.
Метод Эйлера. Пусть дано обыкн. ДУ (1) с нач. усл-ями (2): y¢= f (x, y) у (х0) = у 0
у¢ (х0, у 0) = f (x0, y0)= tg a0. В точке М1 ищем y¢:
у¢ (х1, у 1) = f (x1, y1)= tg a1 .
Полученная ломаная, наз. ломаной линией Эйлера, и есть реш-ем ур-я. При D хі = хі+1 – хі ® 0 и ломанная линия Эйлера ® к истинному решению y= f (x) в силу теоремы Коши.
у 0, у1 = у 0 + f (x0, y0) h,
у2 = у 1 + f (x1, y1) h, … уп+1 = у п + f (xп, yп) h.
Для удобства составляем таблицу
| х | у | f (x, y) | f (x, y) h |
| х0 | у 0 | f (x0, y0) | f (x0, y0) h |
| х1 | у1 | f (x1, y1) | f (x1, y1) h |
| ……. |
 2015-04-20
2015-04-20 640
640








