Тема II. Предел и непрерывность функции
Определения
Ограниченная на множестве Х функция

Неограниченная на множестве Х функция
Функция f(x) называется неограниченной на множестве Х, если:
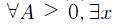
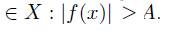
Ограниченная сверху (снизу) функция на множестве Х
Верхняя (нижняя) грань функции на множестве Х
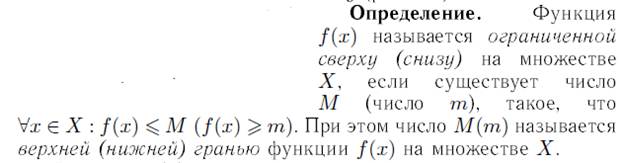
Неограниченная сверху (снизу) функция на множестве Х
Функция f(x) называется неограниченной сверху (снизу) на множестве Х, если: 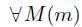
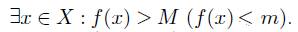
Точная верхняя (нижняя) грань функция на множестве Х
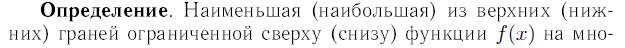
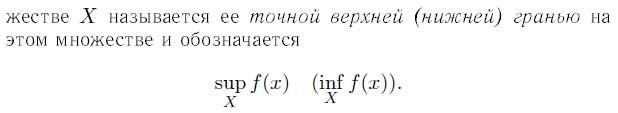
Монотонная на промежутке функция
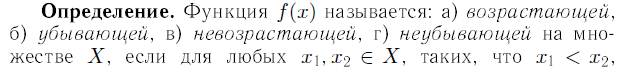
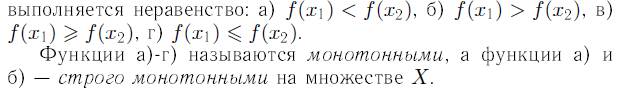
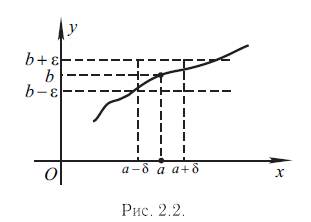
1.12 Предел функции f(x) в точке х=а «по Коши».
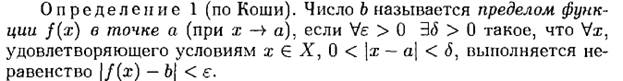


1.13-1.14 Предел функции f(x) в точке х→а+ 0 (справа) и а -0 (слева)«по Коши».
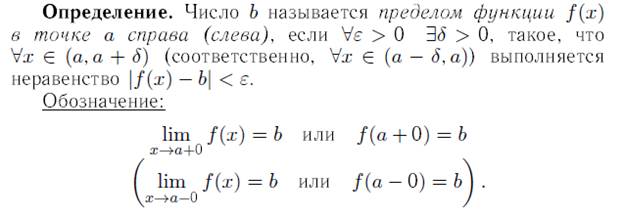
1.15 Предел функции f(x) в точке х→ + ∞ «по Коши».

1.16 Предел функции f(x) в точке х→ - ∞ «по Коши».

1.17 Предел функции f(x) в точке х=а «по Гейне».
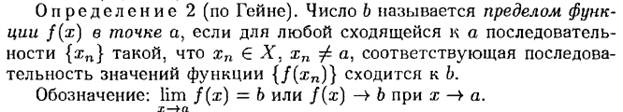
из лекций Быкова:

1.18 Предел функции f(x) в точке х→ + ∞ «по Гейне».
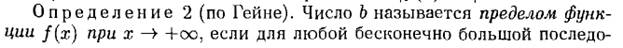

лекция Быкова:

1.19 Предел функции f(x) в точке х→ + ∞ «по Гейне».
Аналогично 1.18
1.20-27 f(x) → + ∞ и f(x) → - ∞ (бесконечно большая функция) при х→а
х→а+ 0, х→а- 0, х→ + ∞ и х→ - ∞ «по Коши»

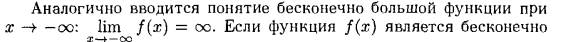
 2015-04-20
2015-04-20 4429
4429