Краевые задачи. Функция Грина

Лекция 13

Как мы говорили ранее, наряду с основной начальной задачей часто приходится решать так называемые краевые или граничные задачи. В этих задачах значение искомой функции задается не в одной, а в двух точках, ограничивающих отрезок, на котором требуется определить решение. Например, в задаче о движении материальной точки массы 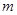под действием заданной силы 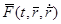часто требуется найти закон движения, если в начальный момент 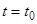точка находилась в положении, характеризуемом радиус-вектором 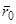, а в момент должна попасть в точку .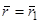

Задача сводится к интегрированию дифференциального уравнения движения 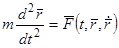с краевыми условиями .

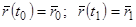Заметим, что эта задача имеет, вообще говоря, не единственное решение. Если речь идет о баллистической задаче и о точках земной поверхности, то в одну и ту же точку тело может попасть по навесной и по настильной траектории. Более того, при очень высоких начальных скоростях можно попасть в ту же точку и после однократного или многократного облета земного шара.

Аналогичную краевую задачу можно поставить и для луча света, проходящего через преломляющую среду: найти направление, по которому луч света должен выйти из точки А, чтобы он попал в другую заданную точку В.

При этом очевидно, что задача не всегда имеет решение, а если решения существуют, то их может быть несколько и даже бесконечное множество (например, если лучи, выходящие из точки А, фокусируются в точке В).

Если удастся найти общее решение дифференциального уравнения краевой задачи, то для решения этой задачи надо определить произвольные постоянные, содержащиеся в общем решении, из граничных условий. При этом, конечно, далеко не всегда существует действительное решение, а если существует, то оно не обязательно единственно.

В качестве примера возникающих здесь возможностей рассмотрим следующую краевую задачу: найти решение уравнения

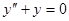, (1)

удовлетворяющее условиям: .

Общее решение уравнения (1) имеет вид 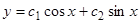. Первое граничное условие удовлетворяется при 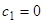, при этом .

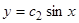Если , где — целое число, то из второго граничного условия находим 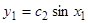, 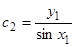. Следовательно, в этом случае существует единственное решение краевой задачи .

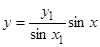Если же 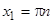и 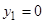, то все кривые пучка 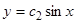являются графиками решения краевой задачи.

При 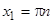, 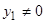решений краевой задачи не существует, так как ни одна кривая пучка 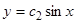не проходит через точку 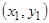, где , .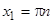

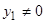Рассмотрим несколько подробнее краевые задачи для линейных уравнений второго порядка

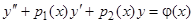, (2)

. (3)

Линейной заменой переменных 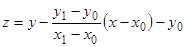краевые условия (3) сводятся к нулевым условиям , причем линейность уравнения (2) не нарушается.

Умножением на 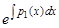линейное уравнение (2) приводится к виду

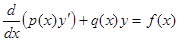, (4)

где 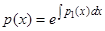. Поэтому без существенного ограничения общности можно заменить изучение краевой задачи (2), (3) изучением краевой задачи для уравнения (4) с граничными условиями

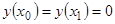. (5)

Вначале рассмотрим краевую задачу (4), (5), причем 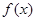является локализованной в точке 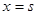функцией с единичным импульсом. Точнее, рассмотрим уравнение

(6)

с граничными условиями 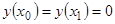, где функция 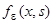равна нулю на всем отрезке 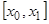, за исключением 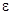-окрестности точки 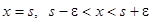, причем 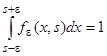. Обозначим 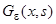непрерывное решение этой краевой задачи и перейдем к пределу при :

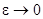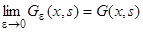. (7)

Нетрудно было бы доказать существование этого предела, не зависящего от выбора функции 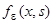, однако в этом нет необходимости, так как пока наши рассуждения носят эвристический характер, а позже мы дадим точное определение функции .

Функция называется функцией влияния или функцией Грина рассматриваемой краевой задачи. Решением рассматриваемой краевой задачи (4), (5) является

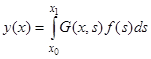. (8)

Функция Грина обладает следующими свойствами, вытекающими из ее определения (7).

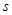1. непрерывна по при фиксированном при , .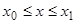

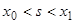2. является решением соответствующего однородного уравнения 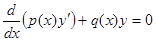на всем отрезке 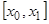, за исключением точки 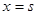(так как вне этой точки в случае локализованной в ней функции правая часть равна нулю).

3. удовлетворяет граничным условиям .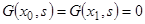

4. В точке 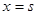производная 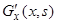должна иметь разрыв первого рода со скачком 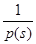. Действительно, ожидать разрыва следует лишь в точке локализации функции, т.е. в точке 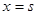. Умножая тождество 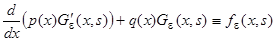на и интегрируя в пределах от 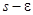до 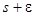, получим 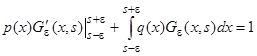и переходя к пределу при 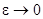, будем иметь .

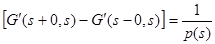Все наши рассуждения о функции Грина носили эвристический характер. Придадим им теперь необходимую точность.

Определение. Функцией Грина краевой задачи (4), (5) называется функция, удовлетворяющая указанным выше условиям 1, 2, 3, 4.

Непосредственной подстановкой в уравнение (4) проверяем, что выражение (8) является решением этого уравнения (краевые условия (5), очевидно, удовлетворяются в силу свойства 3). Действительно,

;

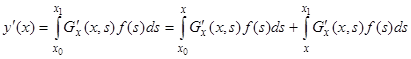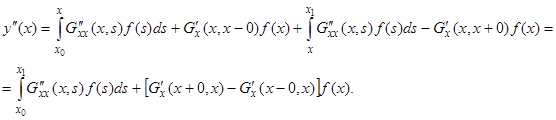
Подставляя (8) в уравнение (4), получим

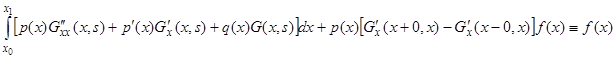в силу условий 2 и 4.

Рассмотрим метод построения функции Грина, из которого получим также достаточное условие ее существования.

Рассмотрим решение 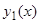уравнения

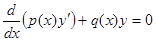, (9)

определяемое начальными условиями 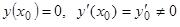. Это решение, вообще говоря, не удовлетворяет второму граничному условию . Случай 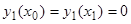является исключительным, и мы его здесь рассматривать не будем.

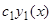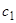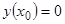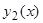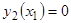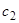Очевидно, что решения , где — произвольная постоянная, также удовлетворяют граничному условию . Аналогично находим нетривиальное решение уравнения (9), удовлетворяющее второму граничному условию . Этому же условию удовлетворяют все решения семейства , где — произвольная постоянная.

Функцию Грина ищем в виде 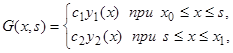причем постоянные 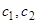выбираем так, чтобы были выполнены условия 1 и 4, т.е. чтобы функция была непрерывна по при фиксированном 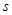, и в частности непрерывна в точке :

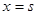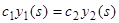, (10)

и чтобы 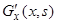в точке 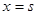имела скачок :

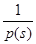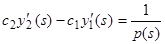. (11)

В силу предположения, что 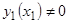, решения 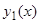и 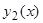линейно независимы, так как все линейно зависимые от 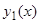решения имеют вид 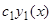и, следовательно, при 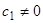не обращаются в нуль в точке 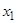, в которой обращается в нуль решение 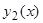.Следовательно, определитель системы (10), (11), являющийся определителем Вронского: 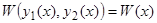в точке 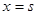, отличен от нуля и постоянные 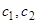, удовлетворяющие системе (10), (11), легко определяются: 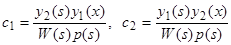, откуда

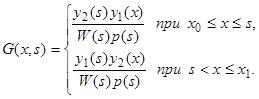(12)

Пример. Найти функцию Грина краевой задачи , , .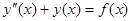

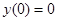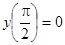Решения соответствующего однородного уравнения, удовлетворяющие условиям 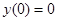, , 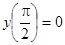соответственно имеют вид 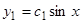и 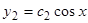, следовательно, согласно (12),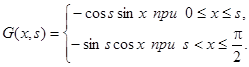

Ранее мы предположили, что не существует нетривиального решения 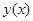однородного уравнения (9), удовлетворяющего нулевым граничным условиям 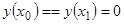. Это условие гарантирует не только существование и единственность решения краевой задачи (4), (5), но и единственность функции Грина.

Действительно, если допустить существование двух различных функций Грина 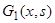и 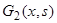для краевой задачи (4), (5), то получим два различных решения этой задач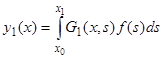и: и 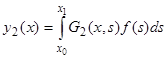, разность которых 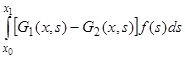, вопреки предположению, будет нетривиальным решением соответствующего однородного уравнения, удовлетворяющим нулевым граничным условиям.