· Функция, непрерывная в точке 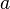 , является ограниченной в некоторой окрестности этой точки.
, является ограниченной в некоторой окрестности этой точки.
· Если функция 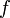 непрерывна в точке
непрерывна в точке 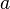 и
и 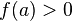 (или
(или 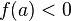 ), то
), то 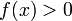 (или
(или 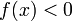 ) для всех
) для всех 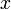 , достаточно близких к
, достаточно близких к 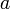 .
.
· Если функции 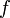 и
и 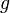 непрерывны в точке
непрерывны в точке 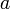 , то функции
, то функции 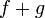 и
и 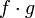 тоже непрерывны в точке
тоже непрерывны в точке 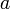 .
.
· Если функции 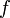 и
и 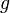 непрерывны в точке
непрерывны в точке 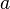 и при этом
и при этом 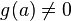 , то функция
, то функция 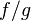 тоже непрерывна в точке
тоже непрерывна в точке 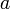 .
.
· Если функция 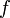 непрерывна в точке
непрерывна в точке 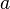 и функция
и функция 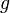 непрерывна в точке
непрерывна в точке 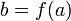 , то их композиция
, то их композиция 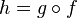 непрерывна в точке
непрерывна в точке 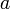 .
.
 2015-04-20
2015-04-20 371
371








