| № | Задания | Варианты ответов |
| | | | | |
| | Указать все уравнения гиперболического типа: А) 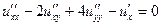 ; Б) ; Б) 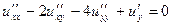 ; В) ; В) 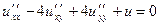 ; Г) ; Г) 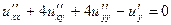 ; Д) ; Д) 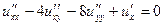 . . | Б | Б,Д | В,Г | А | А,Б |
| 6а | Привести к каноническому виду: 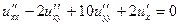 А) А) 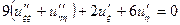 ; Б) ; Б) 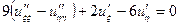 ; В) ; В) 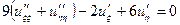 ; Г) ; Г) 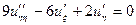 ; Д) ; Д) 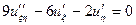 . . | А | Д | Б | В | Г |
| 6б | Указать все возможные семейства характеристик для уравнения: 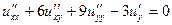 А) А) 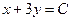 ; ; 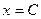 ; Б) ; Б) 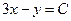 ; ; 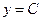 ; В) ; В) 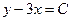 ; ; 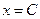 ; Г) ; Г) 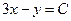 ; ; 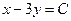 ; Д) ; Д) 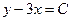 ; ; 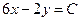 ; Е) ; Е) 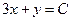 ; ; 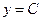 . . | Б,В,Г | А,Е | Б,В | Б,В,Д | Б |
| 7а | Указать все функции, являющиеся решениями дифференциального уравнения 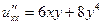 и удовлетворяющие условию и удовлетворяющие условию 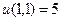 . А) . А) 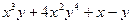 ; Б) ; Б) 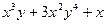 ; В) ; В) 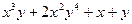 ; Г) ; Г) 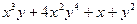 ; Д) ; Д) 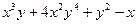 . . | А,В | Б,Г | А,Г | А,Д | Б,Д |
| 7б | Найти общее решение дифференциального уравнения 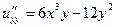 . А) . А) 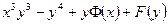 ; Б) ; Б) 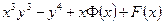 ; В) ; В) 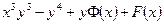 ; Г) ; Г) 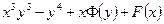 ; Д) ; Д) 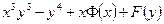 . . | Г | А | В | Б | Д |
| 7в | Общее решение 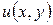 дифференциального уравнения дифференциального уравнения 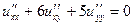 имеет вид: А) имеет вид: А) 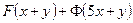 ; Б) ; Б) 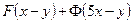 ; В) ; В) 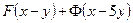 ; Г) ; Г) 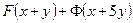 ; Д) ; Д) 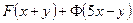 . (Здесь . (Здесь 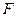 и и 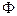 - произвольные функции). - произвольные функции). | В | Г | Б | Д | А |
| 8а | Решить волновое уравнение 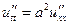 при условии, что при условии, что 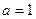 , , 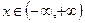 , , 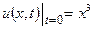 , , 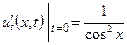 , и найти , и найти 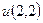 . А) . А) 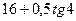 ; Б) ; Б) 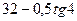 ; В) ; В) 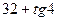 ; Г) ; Г) 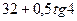 ; Д) ; Д) 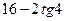 . . | Д | Б | В | А | Г |
| 8б | Решить волновое уравнение 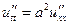 при условии, что при условии, что 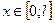 , , 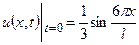 , , 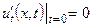 , , 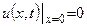 , , 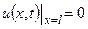 , , 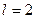 , и найти , и найти 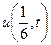 . А) . А) 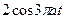 ; Б) ; Б) 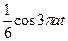 ; В) ; В) 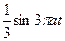 ; Г) ; Г) 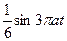 ; Д) ; Д) 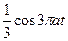 . . | В | Д | Г | Б | А |
| 8в | Решить уравнение теплопроводности 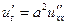 при условии, что при условии, что 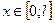 , , 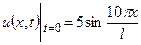 , , 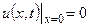 , , 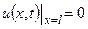 , , 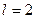 , и найти , и найти 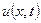 для для 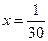 и и 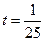 . А) . А) 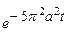 ; Б) ; Б) 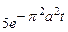 ; В) ; В) 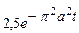 ; Г) ; Г) 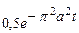 ; Д) ; Д) 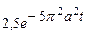 . . | А | Г | Д | В | Б |
| 8г | Решить задачу Коши для уравнения теплопроводности бесконечного стержня 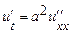 , , 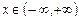 , , 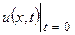 = = 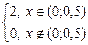 и найти решение при и найти решение при 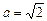 , , 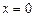 , , 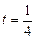 . А) . А) 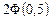 ; Б) ; Б) 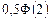 ; В) ; В) 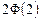 ; Г) ; Г) 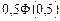 ; Д) ; Д) 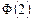 . . | Г | Д | Б | А | В |
| 8д | Найти стационарное распределение температуры 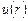 в тонкой пластине, имеющей форму кольца, ограниченного окружностями радиусов в тонкой пластине, имеющей форму кольца, ограниченного окружностями радиусов 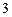 и и 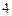 , с граничными условиями: , с граничными условиями: 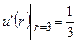 , , 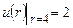 . А) . А) 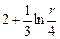 ; Б) ; Б) 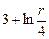 ; В) ; В) 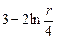 ; Г) ; Г) 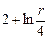 ; Д) ; Д) 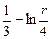 . . | В | Б | А | Г | Д |
| 8е | Найти стационарное распределение температуры 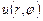 в тонкой пластине, имеющей форму круга радиуса 3, если на границе круга задано условие в тонкой пластине, имеющей форму круга радиуса 3, если на границе круга задано условие 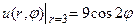 . А) . А) 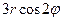 ; Б) ; Б) 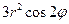 ; В) ; В) 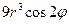 ; Г) ; Г) 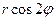 ; Д) ; Д) 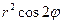 . . | Б | Г | Д | А | В |
| | | | | | | | | | | | | | | | |
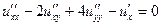 ; Б)
; Б) 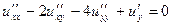 ; В)
; В) 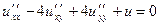 ; Г)
; Г) 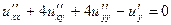 ; Д)
; Д) 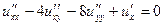 .
. 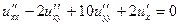 А)
А) 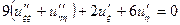 ; Б)
; Б) 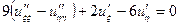 ; В)
; В) 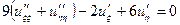 ; Г)
; Г) 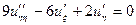 ; Д)
; Д) 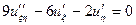 .
. 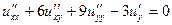 А)
А) 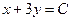 ;
; 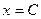 ; Б)
; Б) 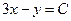 ;
; 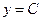 ; В)
; В) 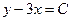 ;
; 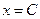 ; Г)
; Г) 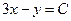 ;
; 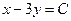 ; Д)
; Д) 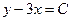 ;
; 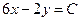 ; Е)
; Е) 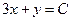 ;
; 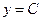 .
. 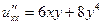 и удовлетворяющие условию
и удовлетворяющие условию 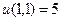 . А)
. А) 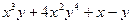 ; Б)
; Б) 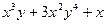 ; В)
; В) 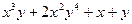 ; Г)
; Г) 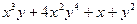 ; Д)
; Д) 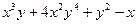 .
. 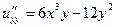 . А)
. А) 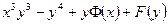 ; Б)
; Б) 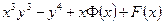 ; В)
; В) 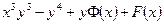 ; Г)
; Г) 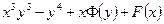 ; Д)
; Д) 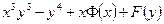 .
. 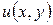 дифференциального уравнения
дифференциального уравнения 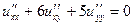 имеет вид: А)
имеет вид: А) 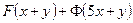 ; Б)
; Б) 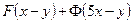 ; В)
; В) 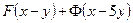 ; Г)
; Г) 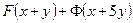 ; Д)
; Д) 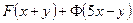 . (Здесь
. (Здесь 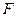 и
и 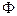 - произвольные функции).
- произвольные функции). 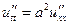 при условии, что
при условии, что 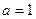 ,
, 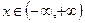 ,
, 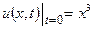 ,
, 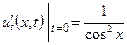 , и найти
, и найти 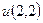 . А)
. А) 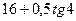 ; Б)
; Б) 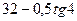 ; В)
; В) 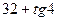 ; Г)
; Г) 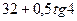 ; Д)
; Д) 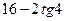 .
. 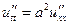 при условии, что
при условии, что 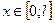 ,
, 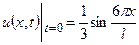 ,
, 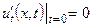 ,
, 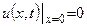 ,
, 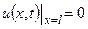 ,
, 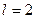 , и найти
, и найти 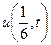 . А)
. А) 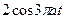 ; Б)
; Б) 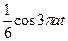 ; В)
; В) 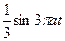 ; Г)
; Г) 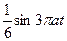 ; Д)
; Д) 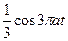 .
. 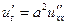 при условии, что
при условии, что 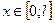 ,
, 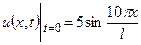 ,
, 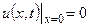 ,
, 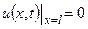 ,
, 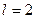 , и найти
, и найти 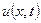 для
для 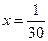 и
и 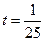 . А)
. А) 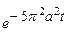 ; Б)
; Б) 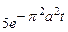 ; В)
; В) 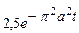 ; Г)
; Г) 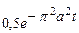 ; Д)
; Д) 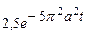 .
. 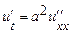 ,
, 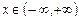 ,
, 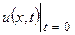 =
= 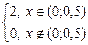 и найти решение при
и найти решение при 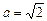 ,
, 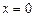 ,
, 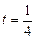 . А)
. А) 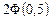 ; Б)
; Б) 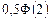 ; В)
; В) 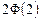 ; Г)
; Г) 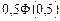 ; Д)
; Д) 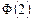 .
. 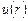 в тонкой пластине, имеющей форму кольца, ограниченного окружностями радиусов
в тонкой пластине, имеющей форму кольца, ограниченного окружностями радиусов 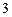 и
и 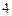 , с граничными условиями:
, с граничными условиями: 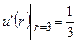 ,
, 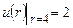 . А)
. А) 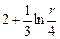 ; Б)
; Б) 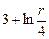 ; В)
; В) 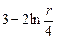 ; Г)
; Г) 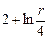 ; Д)
; Д) 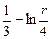 .
. 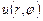 в тонкой пластине, имеющей форму круга радиуса 3, если на границе круга задано условие
в тонкой пластине, имеющей форму круга радиуса 3, если на границе круга задано условие 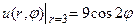 . А)
. А) 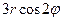 ; Б)
; Б) 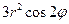 ; В)
; В) 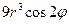 ; Г)
; Г) 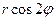 ; Д)
; Д) 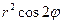 .
.  2015-04-20
2015-04-20 1920
1920








