В разделе рассматриваются следующие задачи: определение типа дифференциального уравнения с частными производными второго порядка, приведение его к каноническому виду, решение дифференциальных уравнений с частными производными.
Задача 1. Определить тип дифференциального уравнения
а) 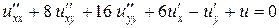 ;
;
б) 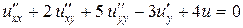 ;
;
в) 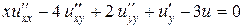 .
.
Решение. Тип дифференциального уравнения вида
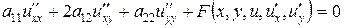 ,
,
где 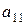 ,
, 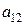 ,
, 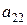 - функции от
- функции от 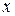 и
и 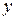 , определяется следующим образом. Уравнение имеет (см. (2.1))
, определяется следующим образом. Уравнение имеет (см. (2.1))
гиперболический тип, если 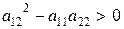 ,
,
параболический тип, если 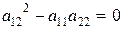 ,
,
эллиптический тип, если 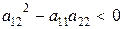 .
.
Рассмотрим случай а): 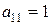 ,
, 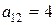 ,
, 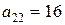 ,
, 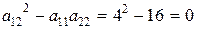 , значит это уравнение параболического типа.
, значит это уравнение параболического типа.
В случае б) 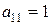 ,
, 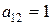 ,
, 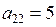 ,
, 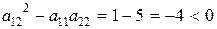 , значит это уравнение эллиптического типа.
, значит это уравнение эллиптического типа.
В случае в) 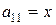 ,
, 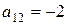 ,
, 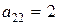 ,
, 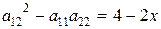 .
.
Выражение 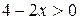 при
при 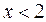 ;
; 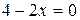 при
при 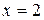 ;
; 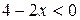 при
при 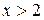 . В соответствии с этим получаем в указанных областях уравнения гиперболического, параболического и эллиптического типов соответственно.
. В соответствии с этим получаем в указанных областях уравнения гиперболического, параболического и эллиптического типов соответственно.
Задача 2. Привести к каноническому виду уравнение
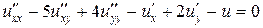 .
.
Решение. Определим тип уравнения:
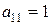 ,
, 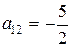 ,
, 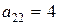 ,
, 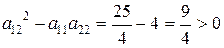 , значит это уравнение гиперболического типа (см.(2.1)). Составим характеристическое уравнение (2.2):
, значит это уравнение гиперболического типа (см.(2.1)). Составим характеристическое уравнение (2.2):
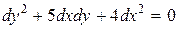 .
.
Найдем его характеристики. Разделив обе части этого уравнения на 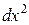 , получим квадратное относительно
, получим квадратное относительно 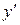 уравнение
уравнение
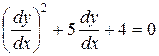 ,или
,или 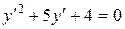 .
.
Решения квадратного уравнения 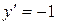 ,
, 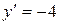 - дифференциальные уравнения первого порядка с разделяющимися переменными. Но тогда справедливы равенства
- дифференциальные уравнения первого порядка с разделяющимися переменными. Но тогда справедливы равенства
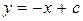 ,
, 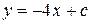 .
.
Записав их в неявном виде, получим общие интегралы соответствующих дифференциальных уравнений. Это и есть характеристики. Таким образом, дифференциальное уравнение гиперболического типа имеет два семейства действительных и различных характеристик:
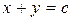 и
и 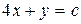 .
.
Если теперь в исходном дифференциальном уравнении с частными производными перейти к новым переменным
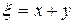 и
и 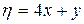 ,
,
то уравнение примет более простую по сравнению с исходной форму – канонический вид. Для гиперболического типа канонический вид выглядит так (2.3):
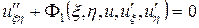 .
.
Конкретизируем его с учетом данных задачи. Так как производные первого порядка от 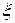 и
и 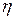 - константы:
- константы:
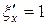 ,
, 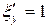 ,
, 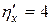 ,
, 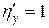 ,
,
то все производные от 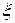 и
и 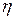 второго порядка равны
второго порядка равны 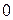 . Тогда согласно формулам (2.7)
. Тогда согласно формулам (2.7)
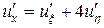 ,
, 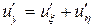 ,
,
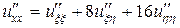 ,
, 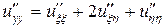 ,
, 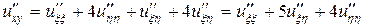 .
.
Подставляя найденные выражения в исходное уравнение, получим
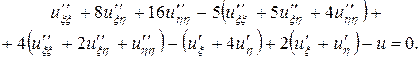
Раскрывая скобки и приводя подобные члены, приходим к уравнению
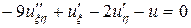 ,или
,или 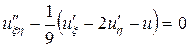 .
.
Сравнивая с (2.3), убеждаемся, что получен канонический вид уравнения.
Задача 3. Привести к каноническому виду уравнение
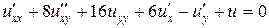
Решение. Это уравнение параболического типа (см. задачу 9а)). Его характеристическое уравнение имеет вид
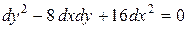 ,или
,или 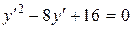 .
.
Решаем его: 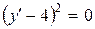 ,
, 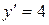 ,
, 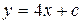 .
.
Записав это решение в неявном виде (в виде общего интеграла), получаем одно семейство действительных характеристик
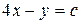 .
.
Выбираем новые переменные. Полагаем 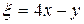 , а в качестве
, а в качестве 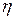 берем достаточно простую функцию (например,
берем достаточно простую функцию (например, 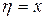 ), не зависимую от
), не зависимую от 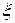 . Последнее означает, что (см. (2.5))
. Последнее означает, что (см. (2.5))
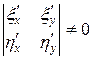 .
.
Для 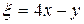 и
и 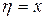 это условие выполняется:
это условие выполняется: 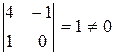 .
.
Делаем замену переменных в исходном уравнении. Так как 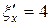 ,
, 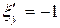 ,
, 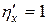 ,
, 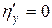 , производные второго порядка от
, производные второго порядка от 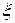 и
и 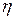 равны
равны 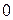 . Тогда с учетом (2.7)
. Тогда с учетом (2.7)
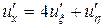 ,
, 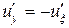
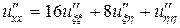 ,
, 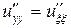 ,
, 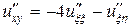 .
.
Подставляем полученные выражения в исходное уравнение
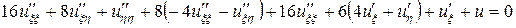 .
.
После преобразований приходим к каноническому уравнению
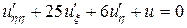 ,
,
что соответствует каноническому виду уравнения параболического типа (2.5):
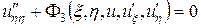 .
.
Задача 4. Привести к каноническому виду уравнение
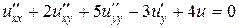 .
.
Решение. Это уравнение эллиптического типа (см. задачу 9б)). Его характеристическое уравнение имеет вид:
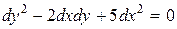 , или
, или 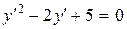 .
.
Решая последнее уравнение, получим
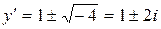 ,
, 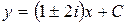 .
.
Общий интеграл имеет вид
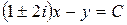 ,
,
что соответствует двум семействам комплексно сопряженных характеристик (с учетом знака). Для приведения исходного уравнения к каноническому виду в качестве новых переменных 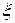 и
и 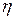 следует взять (см. (2.6)) действительную и мнимую части выражения
следует взять (см. (2.6)) действительную и мнимую части выражения
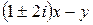 ,
,
а именно: 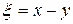 ,
, 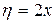 .
.
Вычисляем необходимые для подстановки производные:
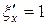 ,
, 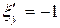 ,
, 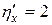 ,
, 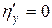 ,
, 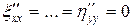 .
.
Согласно (2.7) имеем
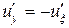 ,
, 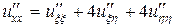 ,
, 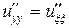 ,
, 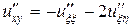 .
.
Подставляя полученные выражения в исходное уравнение, приходим к каноническому виду:
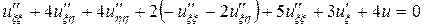 ,
,
или 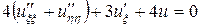 , или
, или 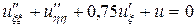 ,
,
что соответствует общему случаю (2.6):
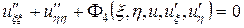 .
.
Задача 5. Среди представленных функций найти решения дифференциального уравнения 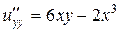 , удовлетворяющие условию
, удовлетворяющие условию 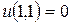 :
:
а) 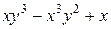 ; б)
; б) 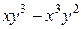 ;в)
;в) 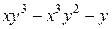 ;
;
г) 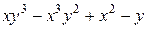 ; д)
; д) 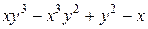 .
.
Решение. Проверим сначала, какие функции удовлетворяют условию 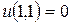 :
:
а) 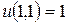 ; б)
; б) 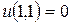 ; в)
; в) 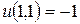 ; г)
; г) 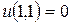 ; д)
; д) 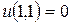 .
.
Итак, условие выполняется в случаях б), г) и д).
Находим 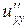 для каждой функции:
для каждой функции:
б) 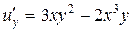 ,
, 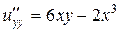 ;
;
г) 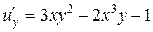 ,
, 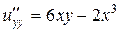 ;
;
д) 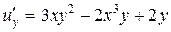 ,
, 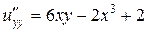 .
.
Таким образом, две функции (б и г) являются решениями дифференциального уравнения.
Задача 6. Найти общее решение дифференциального уравнения
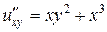 .
.
Решение. Так как 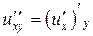 , дифференциальное уравнение можно записать следующим образом
, дифференциальное уравнение можно записать следующим образом
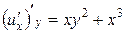
и найти 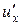 интегрированием по
интегрированием по 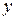 :
:
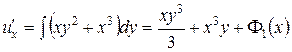 .
.
Здесь 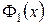 - произвольная функция, появляется из-за того, что неопределенный интеграл вычисляется с точностью до константы, но при интегрировании по
- произвольная функция, появляется из-за того, что неопределенный интеграл вычисляется с точностью до константы, но при интегрировании по 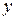 в роли константы выступает величина
в роли константы выступает величина 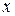 .
.
Последнее равенство интегрируем по 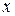 и получаем искомую функцию
и получаем искомую функцию 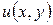 :
:
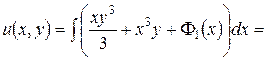
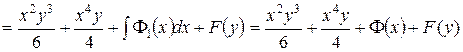 ,
,
где 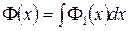 ;
; 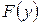 - произвольная функция, появляется при интегрировании по
- произвольная функция, появляется при интегрировании по 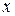 , когда
, когда 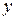 играет роль константы. Итак,
играет роль константы. Итак,
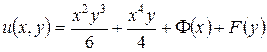 .
.
Задача 7. Найти общее решение дифференциального уравнения
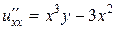 .
.
Решение. 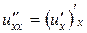 , поэтому уравнение запишется так:
, поэтому уравнение запишется так: 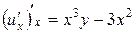 .
.
Интегрируем это равенство дважды по 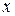 :
:
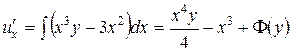 ,
,
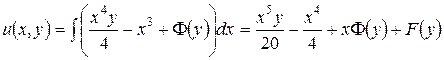 ,
,
где 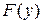 и
и 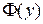 - две произвольные функции, появляются при интегрировании по
- две произвольные функции, появляются при интегрировании по 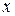 , когда
, когда 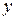 выступает в роли константы.
выступает в роли константы.
Задача 8. Найти общее решение дифференциального уравнения
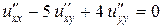 .
.
Решение. Согласно формулам (2.1) вычисляем
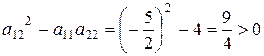
и делаем вывод, что исходное уравнение гиперболического типа. Его характеристическое уравнение
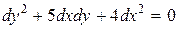 ,
,
рассмотренное в задаче 2, имеет два семейства характеристик:
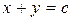 и
и 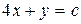 ,
,
значит канонический вид можно получить сделав замену
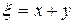 и
и 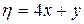 .
.
Подставив полученные в задаче 2 выражения для производных в исходное уравнение, получим:
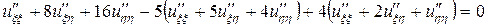 ,
,
или 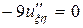 , откуда
, откуда 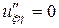 .
.
Заметим, что если исходное уравнение имеет вид (2.8)
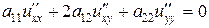 ,
,
где 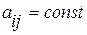 , причем
, причем 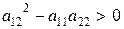 (гиперболическое), то с помощью указанной замены переменных оно приводится к каноническому виду
(гиперболическое), то с помощью указанной замены переменных оно приводится к каноническому виду
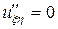 .
.
Решаем последнее уравнение. Его можно записать так: 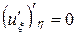 . Но если производная от какой-либо функции равна
. Но если производная от какой-либо функции равна 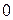 , то эта функция - константа, т.е.
, то эта функция - константа, т.е. 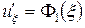 (
(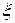 при этом выступает в роли константы). Теперь интегрируем по
при этом выступает в роли константы). Теперь интегрируем по 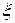 (константой является
(константой является 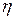 ):
):
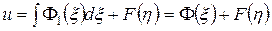 .
.
Здесь 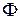 и
и 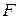 - две произвольные функции. Подставляя в полученное равенство найденные ранее
- две произвольные функции. Подставляя в полученное равенство найденные ранее 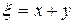 и
и 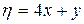 , окончательно получаем
, окончательно получаем
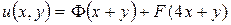 .
.
Задача 9. Решить задачу Коши для волнового уравнения 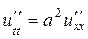 ,
, 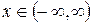 ,
, 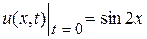 ,
, 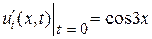 при
при 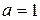 и найти
и найти 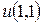 .
.
Решение. Воспользуемся формулой Даламбера (2.9):
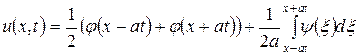 ,
,
где 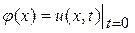 ,
, 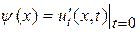 . Так как
. Так как 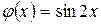 ,
, 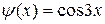 ,
, 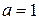 , получим
, получим
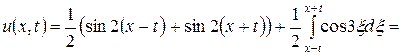
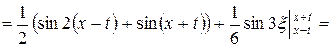
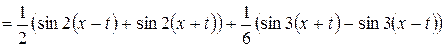 .
.
Тогда 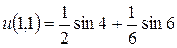 .
.
Задача 10. Решить смешанную задачу для волнового уравнения 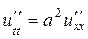 ,
, 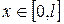 ,
, 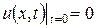 ,
, 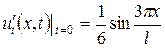 ,
, 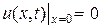 ,
, 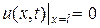 при
при 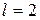 и определить закон движения точки с абсциссой
и определить закон движения точки с абсциссой 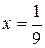 .
.
Решение. Решение смешанной задачи для волнового уравнения имеет вид (2.10):
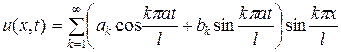 ,
,
где 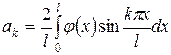 ,
, 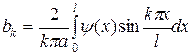 ,
, 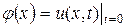 ,
, 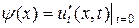 .
.
Согласно условиям задачи 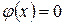 , но тогда
, но тогда 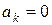 при любом
при любом 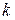 .
.
Найдем 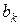 . Поскольку
. Поскольку 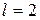 ,
, 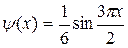 , значит
, значит
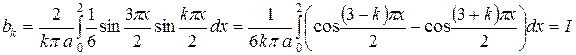 .
.
Обозначив последний интеграл 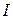 , рассмотрим два случая:
, рассмотрим два случая: 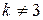 и
и 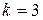 . Если
. Если 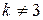 , то:
, то:
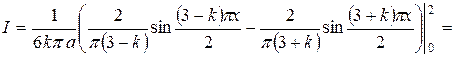
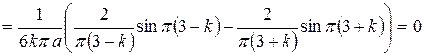 .
.
При 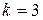 возвращаемся к интегралу, так как последние выражения, содержащие
возвращаемся к интегралу, так как последние выражения, содержащие 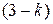 в знаменателе, в этом случае не существуют. Получаем
в знаменателе, в этом случае не существуют. Получаем
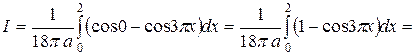
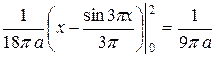 .
.
Итак, 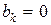 для всех
для всех 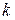 , кроме
, кроме 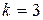 , а
, а 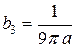 . Но тогда решение
. Но тогда решение 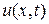 представляет собой не бесконечную сумму, а лишь одно слагаемое, соответствующее
представляет собой не бесконечную сумму, а лишь одно слагаемое, соответствующее 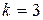 :
:
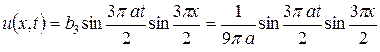 .
.
Осталось подставить в это выражение 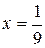 :
:
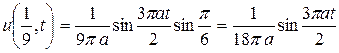 .
.
Задача 11. Решить смешанную задачу для уравнения теплопроводности 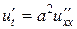 ,
, 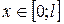 ,
, 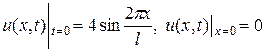 ,
, 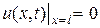 и найти решение при
и найти решение при 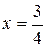 ,
, 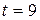 ,
, 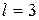 .
.
Решение. Решение смешанной задачи для уравнения теплопроводности имеет вид (2.11):
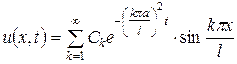 ,
,
где 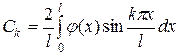 ,
, 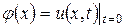 .
.
Так как 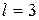 ,
, 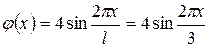 . Найдем
. Найдем 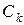 .
.
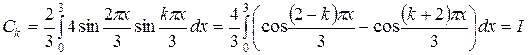 .
.
Обозначив последний интеграл 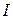 , рассмотрим два случая:
, рассмотрим два случая: 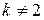 и
и 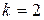 .
.
Если 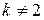 , то
, то
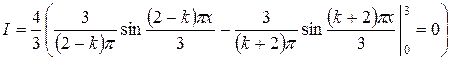 .
.
При 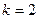 предыдущее выражение, содержащее
предыдущее выражение, содержащее 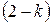 в знаменателе, не существует, поэтому возвращаемся к интегралу. Получаем
в знаменателе, не существует, поэтому возвращаемся к интегралу. Получаем
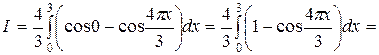
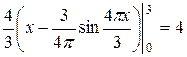 .
.
Таким образом, 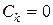 для всех
для всех 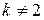 , а
, а 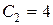 . Но тогда решение
. Но тогда решение 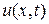 представляет собой не бесконечную сумму, а лишь одно слагаемое, соответствующее
представляет собой не бесконечную сумму, а лишь одно слагаемое, соответствующее 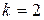 , и равно
, и равно
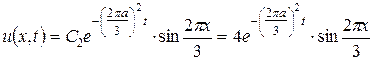 .
.
При 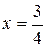 ,
, 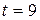 это решение принимает вид:
это решение принимает вид:
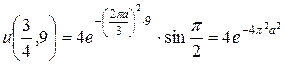 .
.
Задача 12. Решить задачу Коши для уравнения теплопроводности бесконечного стержня: 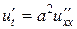 ,
, 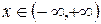 ,
, 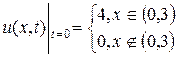 и найти решение при
и найти решение при 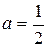 ,
, 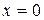 ,
, 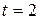 .
.
Решение. Решение находим по формуле (2.12), называемой интегралом Пуассона:
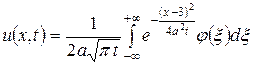 ,
,
где 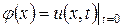 .
.
Так как 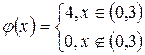 , то
, то 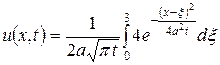 .
.
Подставив 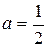 ,
, 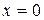 ,
, 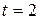 , получим
, получим
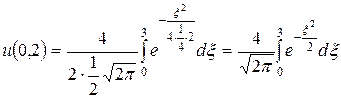 .
.
Полученный результат можно представить с помощью функции Лапласа
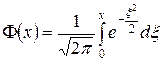
следующим образом: 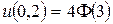 (таблица значений функции Лапласа приводятся во многих учебниках – см., например, В.Е.Гмурман. Руководство к решению задач по теории вероятностей и математической статистике).
(таблица значений функции Лапласа приводятся во многих учебниках – см., например, В.Е.Гмурман. Руководство к решению задач по теории вероятностей и математической статистике).
Задача 13. Найти стационарное распределение температуры 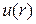 в тонкой пластине, имеющей форму кольца, ограниченного окружностями радиусов 2 и 3, с граничными условиями
в тонкой пластине, имеющей форму кольца, ограниченного окружностями радиусов 2 и 3, с граничными условиями 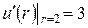 ,
, 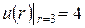 .
.
Решение. Воспользуемся уравнением Лапласа в полярных координатах (2.13):
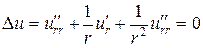 .
.
Из условий задачи следует, что искомая функция 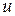 не зависит от изменения
не зависит от изменения 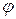 , поэтому уравнение принимает вид:
, поэтому уравнение принимает вид:
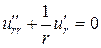 ,или
,или 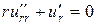 , или
, или 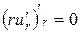 .
.
Интегрируя это равенство по 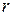 , получим:
, получим:
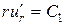 , откуда
, откуда 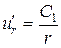 , или
, или 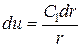 .
.
Еще раз проинтегрируем: 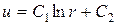 .
.
Произвольные постоянные 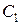 и
и 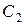 находим из граничных условий:
находим из граничных условий:
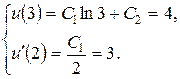
Из второго уравнения находим 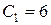 и подставляем в первое:
и подставляем в первое: 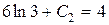 , значит,
, значит, 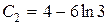 . При этом решение
. При этом решение 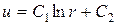 принимает вид:
принимает вид:
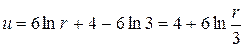 .
.
Задача 14. Найти стационарное распределение температуры в тонкой пластине, имеющей форму круга радиуса 2, если на границе круга задано условие 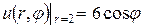 .
.
Решение. Стационарное распределение температуры в полярных координатах описывается уравнением Лапласа
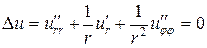 .
.
Это уравнение и граничные условия вида 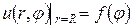 образуют задачу Дирихле для круга с решением (2.14):
образуют задачу Дирихле для круга с решением (2.14):
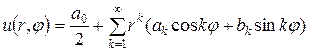 ,
,
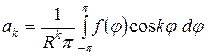 ,
, 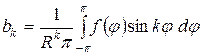 .
.
Для 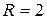 и
и 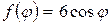 , получаем
, получаем
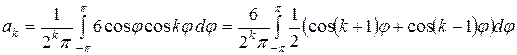 .
.
Этот интеграл равен 0 для всех неотрицательных 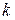 , кроме
, кроме 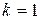 (см. задачи 18, 19). Для
(см. задачи 18, 19). Для 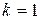 имеем:
имеем:
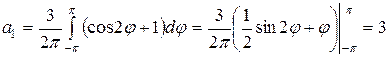 .
.
Вычисляем 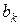 :
:
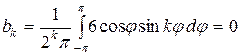
как интеграл от нечетной функции по симметричному отрезку 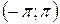 .
.
Тогда решение задачи имеет вид 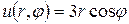 .
.
 2015-04-20
2015-04-20 21360
21360