Необходимое условие линейной независимости системы векторов (в координатах)

Теорема (необходимое и достаточное условие линейной независимости в координатной форме). Cистема векторов 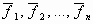из Rⁿ линейно независима тогда и только тогда, когда отличен от нуля определитель, строками (столбцами) которого являются компоненты векторов системы:

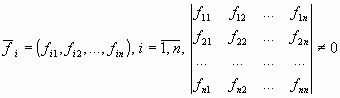
Теорема доказана на лекции.

Следствиями из этой теоремы являются следующие утверждения:

1. если 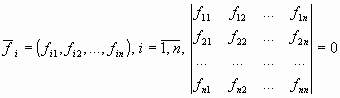, то система векторов 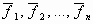из Rⁿ — линейно зависима;

2. любая система векторов 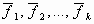из Rⁿ, k > n — линейно зависима.

2.2. Размерность пространства R ⁿ. Базис в R ⁿ