Рассмотрим функцию у=ƒ(х). Формула Тейлора позволяет, при определенных условиях, приближенно представить функцию ƒ(х) в виде многочлена и дать оценку погрешности этого приближения.
Теорема. Если функция ƒ(х) определена в некоторой окрестности точки х0 и имеет в ней производные до (n+1)-го порядка включительно, то для любого х из этой окрестности найдется точка сє(х0;х) такая, что справедлива формула
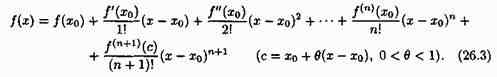
Формула (26.3) называется формулой Тейлора для функции ƒ(х). Эту формулу можно записать в виде ƒ(х)=Рn(х)+Rn(x), где
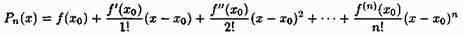
называется многочленом Тейлора, а
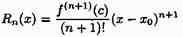
называется остаточным членом формулы Тейлора, записанным в форме Лагранжа. Rn(х) есть погрешность приближенного равенства ƒ(х)≈Рn(х). Таким образом, формула Тейлора дает возможность заменить функцию у=ƒ(х) многочленом у=Рn(х) с соответствующей степенью точности, равной значению остаточного члена Rn(x).
45. Функции двух переменных. Определение. Геометрический смысл.
Если любой паре упорядоченных чисел (x, y) из некоторого множества D поставлено в соответствие единственное число z, то переменная z называется функцией двух переменных. z = f (x, y). Переменную z называют зависимой переменной, а переменные x и y – независимыми. Множество D называется областью определения функции, а множество z – множеством значений функции.
Геометрический смысл – множество значений функции представляет собой некоторую поверхность. Так, с помощью уравнения z=x^2+y^2 мы получим параболоид.
46. Частные производные и производные высших порядков.
Частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.
Производные высших порядков - 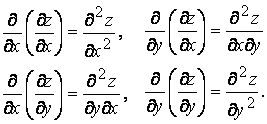 . Подобные формулы посмотреть в тетради, там написано понятней.
. Подобные формулы посмотреть в тетради, там написано понятней.
47. Дифференциал функции двух переменных.
Полным дифференциалом 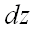 функции
функции 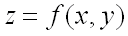 называется линейная, относительно
называется линейная, относительно 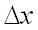 и
и 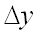 ) часть полного приращения функции:
) часть полного приращения функции: 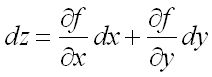 .
.
Следовательно, для выполнения задания достаточно найти частные производные первого порядка от функции и подставить их в вышеприведенную формулу.
48. Дифференцирование неявной функции двух переменных.
Если в уравнении вида 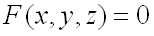 каждой паре чисел
каждой паре чисел 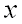 и
и 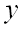 из некоторой области соответствует одно или несколько значений
из некоторой области соответствует одно или несколько значений 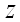 , удовлетворяющих этому уравнению, то уравнение
, удовлетворяющих этому уравнению, то уравнение 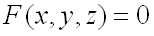 неявно определяет одну или несколько однозначных функций
неявно определяет одну или несколько однозначных функций 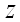 от
от 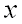 и
и 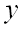 . В этом случае говорят, что
. В этом случае говорят, что 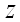 есть неявная функция от
есть неявная функция от 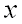 и
и 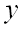 .
.
Частные производные 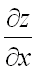 и
и 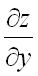 неявной функции находятся по формулам (предполагается, что
неявной функции находятся по формулам (предполагается, что 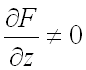 ):
):
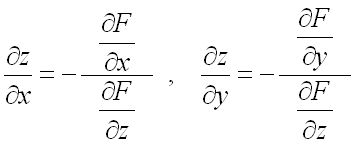
49. Экстремумы функции двух переменных. Необходимое и достаточное условия экстремума
Необходимое условие:
Если функция 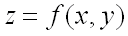 достигает экстремума при
достигает экстремума при 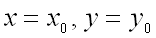 , то каждая частная производная первого порядка от
, то каждая частная производная первого порядка от 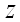 или обращается в нуль при этих значениях аргументов, или не существует.
или обращается в нуль при этих значениях аргументов, или не существует.
Достаточное условие:
Пусть в некоторой области, содержащей точку 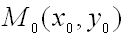 функция
функция 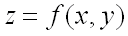 имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка
имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка 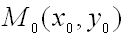 является критической точкой функции
является критической точкой функции 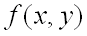 , т.е.
, т.е.
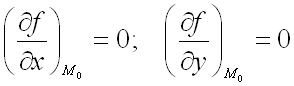 ,
,
тогда при 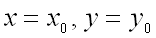 :
:
1) 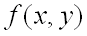 имеет максимум, если дискриминант
имеет максимум, если дискриминант 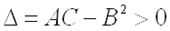 и
и 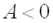 , где
, где 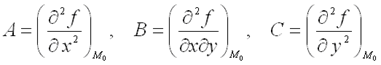 ;
;
2) 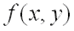 имеет минимум, если дискриминант
имеет минимум, если дискриминант 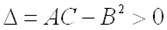 и
и 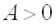 ;
;
3) 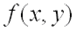 не имеет ни минимума, ни максимума, если дискриминант
не имеет ни минимума, ни максимума, если дискриминант 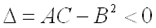 ;
;
4) если  , то экстремум может быть, а может и не быть (требуется дополнительное исследование).
, то экстремум может быть, а может и не быть (требуется дополнительное исследование).
50. Вектор градиент и его свойства.
Градиентом дифференцируемой функции u = u (x;y) (u = u(x;y;z)) называется вектор, перпендикулярный к линии (поверхности) уровня функций u = u (x;y) (u = u (x;y;z)):
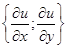 | |||
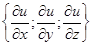 |
grad u (х;у) = в R(2); grad u (х;у; z) = в R(3).
Пример 2. Найти градиент функции u(x;y) = x2 + y к линии уровня при с = 1 в точках А(0;1) и В(1;0).
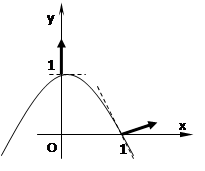 |
Уравнения линий уровня х2 + у = с.
Выделим из семейства линий уровня линию
при с = 1: х2 + у =1. Это парабола
у =1 – х2 с вершиной в точке (0;1) и ветвями,
направленными вниз.
Найдем градиент в произвольной точке:
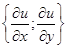 |
grad u (х;у) = = {2x; 1};
в точке А(0;1): grad u (х;у) = {0; 1}; в точке В(1;0): grad u (х;у) = {2; 1} и они перпендикулярны к линии уровня в данных точках.
Производная по направлению вектора 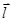 .
.
Пусть в области D задана скалярная функция u = u(x;y;z) и выделена поверхность уровня u(x;y;z)=с, на которой взята точка М(х;y;z).
Из точки М проведем вектор 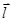 ={x;y;z}, на котором выделим
={x;y;z}, на котором выделим 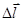 .
.
Спроектируем 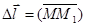 на плоскость
на плоскость 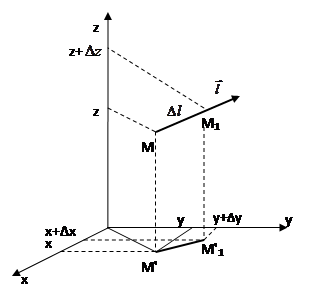 xoy: прxoyΔl=М'М'1. Нормируем вектор
xoy: прxoyΔl=М'М'1. Нормируем вектор 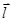 (
(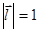 ):
):
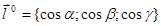 , где
, где 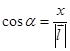 ,
, 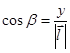 ,
, 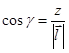 ,
, 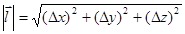 .
.
Запишем полное приращение 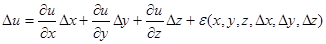
для u(x;y;z), где ε(x,y,z,Δx,Δy,Δz) – бесконечно малая более высокого порядка.
Разделим приращение Δu на 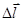
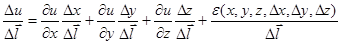 .
.
Переходя к пределу при 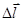 → 0, будем иметь значение производной по направлению вектора
→ 0, будем иметь значение производной по направлению вектора 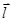 в R(3):
в R(3): 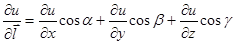 .
.
Производная по направлению – скорость роста функции u(x;y;z) по направлению вектора 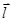 .
.
 2015-04-20
2015-04-20 4006
4006
