Замечание

Предел функции f(x) при 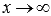бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной.

Обозначается .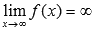

12. Бесконечно малые величины. Связь с пределами функций.

Функция α (x) называется бесконечно малой при 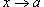, если

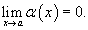
Предположим, что α (x) и β (x) - бесконечно малые функции при .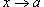

· Если 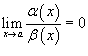, то говорят, что функция α (x) является бесконечно малой высшего порядка по сравнению с функцией β (x);

· Если 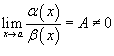, то говорят, что функции α (x) и β (x) являются бесконечно малыми одинакового порядка малости;

· Если 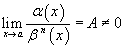, то говорят, что функция α (x) является бесконечно малой порядка относительно функции β (x);

· Если 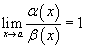, то говорят, что бесконечно малые функции α (x) и β (x) эквивалентны при .

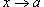13. Свойства бесконечно малых величин

1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2)Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.

3)Произведение двух бесконечно малых функций есть функция бесконечно малая.

4)Произведение бесконечно малой функции на число есть функция бесконечно малая.

5)Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.

14. Связь бесконечно малой и бесконечно большой величин.

Теорема. Пусть 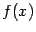-- функция, бесконечно большая при базе 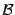. Тогда величина 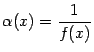-- бесконечно малая при базе .

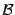15. Теорема о пределе суммы конечного числа функций, имеющих предел при x->x0

Предел алгебраической суммы конечного числа функций, имеющих в данной точке конечный предел, равен алгебраической сумме пределов этих функций в этой же точке

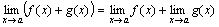
16. Теорема о единственности предела функции

Числовая последовательность может иметь только один предел

17. Теорема о пределе произведении конечного числа функций, имеющих предел при x->x0

Предел произведения конечного числа функций равен произведению пределов этих функций.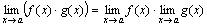

18. Теорема о пределе частного двух функций при условии, что предел знаменателя равен нулю.

Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля.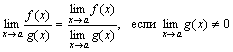

Но если предел знаменателя стремиться к нулю, то в исходном пределе получаем, что предел будет равен 1/0. Ввиду чего предел частного двух функций, где предел знаменателя равен нулю будет равен бесконечности.

19. Предельный переход в неравенствах.

Если элементы сходящейся последовательности { x_n }, начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b (x_n ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

Замечание. Элементы сходящейся последовательности { x_n } могут удовлетворять строгому неравенству x_n > b, однако при этом предел a может оказаться равным b. Например, если 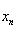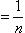, то x_n > 0, однако .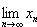

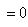20. Признак существования предела последовательности. Число е. Натуральные логарифмы.

Числовая последовательность (x_n) имеет конечный предел тогда и только тогда, когда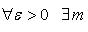

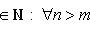
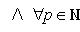
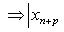
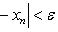
Последовательность 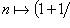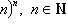, имеет конечный предел, называемый числом е:

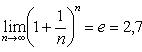
Натуральный логарифм — это логарифм по основанию e

21. Первый замечательный предел.

Замечательные пределы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

· Первый замечательный предел:

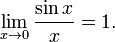
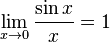
Следствия

·

·

·

·

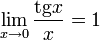
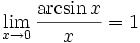
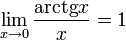
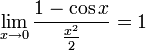
22. Второй замечательный предел. Привести примеры.

Справка: 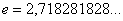– это иррациональное число.

имеет вид:

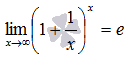
или в другой записи

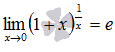
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность .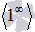

ЗАМЕЧАНИЕ Неопределенность единица в степени бесконечность 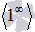является степенной неопределенностью, так что может быть раскрыта по правилам нахождения пределов показательно степенных функций.

23. Непрерывность функции в точке. Свойства функций, непрерывных в точке.

Функция f(x) называется непрерывной в точке 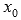, если предел слева равен пределу справа и совпадает со значением функции в точке 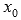, то есть .

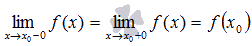1 свойство: если функци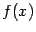и и 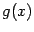непрерывны в точке 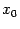, то функции 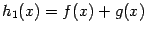, , 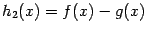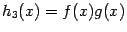непрерывны в точке 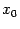. Если 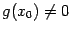, то функция 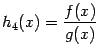также непрерывна в точке .

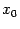2 свойство: Суперпозиция непрерывных функций – есть непрерывная функция.

24. Свойства функций, непрерывных на отрезке.

Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897) - немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке 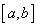выполняется условие - .

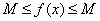Свойство 2: Функция, непрерывная на отрезке 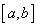, принимает на нем наибольшее и наименьшее значения.

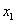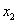Т.е. существуют такие значения и , что 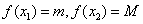, причем .

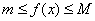Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке 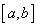, принимает на этом отрезке все значения между двумя произвольными величинами.

Свойство 4: Если функция 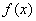непрерывна в точке 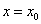, то существует некоторая окрестность точки 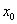, в которой функция сохраняет знак.

Свойство 5: (Первая теорема Больцано (1781-1848) - Коши). Если функция 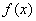- непрерывная на отрезке 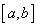и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где .

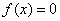25. Определение производной. Геометрический и механический смысл производной

Пусть в некоторой окрестоности точки 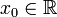определена функция 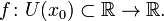Производной функции 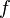в точке 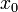называется предел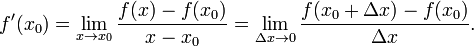

Геометрический смысл производной:

Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке. Для любых двух точек A и B графика функции: f’ (x)= tg 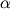, где 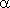- угол наклона секущей AB.

Физический смысл производной:

Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки: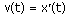

26. Определение производной. Экономический смысл производной.

Пусть в некоторой окрестоности точки 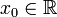определена функция 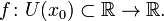Производной функции 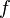в точке 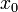называется предел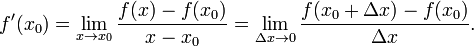

Экономический смысл производной:

Производительность труда есть производная от объема произведенной продукции по времени

27. Связь понятия непрерывности функции в данной точке и дифференцируемостью в этой точке.

Если функция y = f (x) дифференцируема в точке x 0, то она и непрерывна в этой точке.
Обратное утверждение не будет верным.

28. Правила дифференцирования.

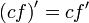
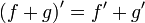
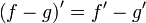
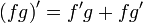
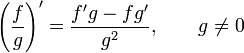
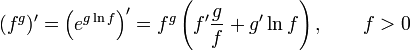
29. Производная сложной функции.

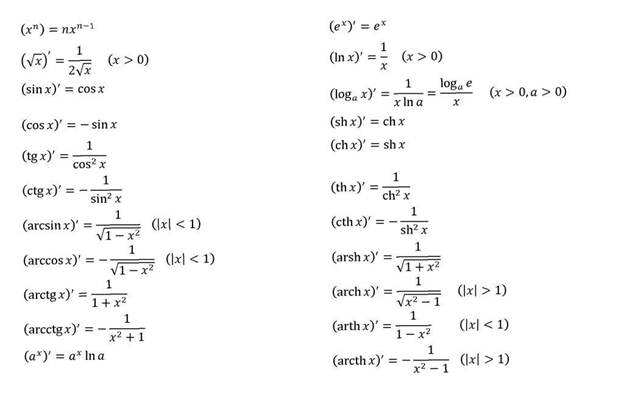
В производная сложной функции (f(g(x)))’ = f’(g(x))*g’(x)*x’

30. Производная обратной функции. (y=arcsin x)

См. таблицу выше

31. Производная логарифмической функции

См. таблицу

32. Производная степенно-показательных функций.

См. таблицу

33. Теорема Ролля.

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.

34. Теорема Лагранжа.

Согласно теореме Лагранжа, если функция f (x) непрерывна на отрезке [ a; b ] и дифференцируема на интервале (a; b), то существует хотя бы одна точка 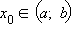такая, что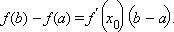

35. Теорема Лопиталя.

Если 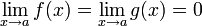или =∞, т.е. [0/0] или [∞/∞], то

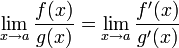
36. Достаточное условие возрастания и убывания функции.

Для того, чтобы функция f(x) возрастала (убывала) в точке х0, достаточно чтобы f’(x0)>0 (f’(x0)<0)

37. Экстремумы функции. Необходимое условие.

Если ф-ия f(x) имеет экстремум в точке x0, то производная её в этой же точке равна нулю или не существует. Доказательство очевидно.

38. Достаточные условия экстремума функции.

Первый признак.

Дополним, что точки, где производная равна нулю, называются стационарными; а точки, где производная не существует называются критическими. Итак, если точка х₀ есть стационарная точка для функции f(x) или если в этой точке не существует для неё двусторонней конечной производной, то точка х₀представляется, так сказать лишь “подозрительной” по экстремуму и подлежит дальнейшему испытанию.

Подставляя в производную f’(x) сначала х<х₀, а затем х>х₀, устанавливаем знак производной вблизи от точки х₀ слева и справа от неё; если при этом производная f’(x) меняет знак плюс на минус, то налицо максимум, если меняет знак с минуса на плюс, то – минимум; если же знака не меняет, то экстремума вовсе нет.

Достаточное условие. Второй признак.

Теорема 3.1:Если х₀ есть стационарная точка функции f(x) и f’’(x)<0, то в точке х₀функция иммет максимум,а если f’’(x)>0, то функция имеет в точке х₀ минимум.

Доказательство: По определению второй производной

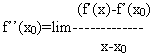
· если f’’(x)>0, то х₀ – точка минимума функции;

· если f’’(x)<0, то х₀ – точка максимума функции.

Замечание 1: если f’’(x)=0,то это правило теряет силу и нужно воспользоваться первым признаком нахождения экстремумов. При этом экстремум может существовать, а может и не существовать.

Однако в случае своей применимости второй признак оказывается весьма удобным: вместо рассмотрения знака функции f’(x) в точках, отличных от предполагаемой точки экстремума, он позволяет дать ответ по знаку функции f’’(x) в той же точке.

39. Наибольшее и наименьшее значение функции на отрезке.

Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Правило нахождения наибольшего и наименьшего значений функции на отрезке[ a, b ]:

1. Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.

2. Вычислить значения функции на концах отрезка при x = a, x = b.

3. Из всех полученных значений выбрать наибольшее и наименьшее.

40. Выпуклость графика функции. Точки перегиба.

Функция f (x) называется выпуклой на интервале (a, b), если её график на этом интервале лежит ниже касательной, проведенной к кривой y = f (x) в любой точке (x ₀, f (x ₀)), x ₀ 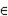(a, b)

Функция f (x) называется вогнутой на интервале (a, b), если её график на этом интервале лежит выше касательной, проведенной к кривой y = f (x) в любой точке (x ₀, f (x ₀)), x ₀ 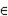(a, b).