1. Производная по направлению имеет наибольшее значениепо направлению градиента, что следует из коллинеарности 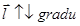 , то есть cos 0 = 1 и
, то есть cos 0 = 1 и 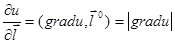 .
.
2. Производная по направлению равна нулю по направлению, перпендикулярному градиенту, что следует из ортогональности 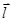
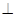 grad u, то есть cos (π/2) = 0 и
grad u, то есть cos (π/2) = 0 и 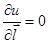 .
.
Замечания. 1) Другие обозначения градиента функции:
grad u = gr u = 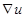 , где вектор
, где вектор 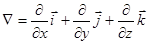 называется оператор Гамильтона или оператор набла.
называется оператор Гамильтона или оператор набла.
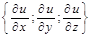 Тогда
Тогда 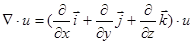 =
= 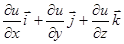 = – разные формы записи градиента.
= – разные формы записи градиента.
1) 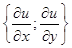 Если функция u = u(x,y)
Если функция u = u(x,y) 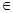 R(2), то градиент функции – это вектор
R(2), то градиент функции – это вектор 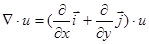 =
= 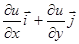 =,
=,
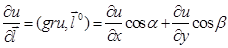 а производная по направлению – число, равное.
а производная по направлению – число, равное.
Пример 3. Найти производную функции u = x2 + y2 + z2 по
направлению вектора 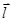 = {2;1;-2} в точке М(1;1;1).
= {2;1;-2} в точке М(1;1;1).
Производную функции u = x2 + y2 + z2 по направлению вектора
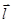 ={2;1;-2}
={2;1;-2}
найдем по определению 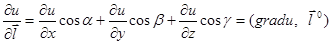 .
.
Вычислим градиент grad u = 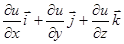 = {2x; 2y; 2z} в произвольной точке, а затем в точке М(1;1;1): grad u (М) = {2; 2; 2}.
= {2x; 2y; 2z} в произвольной точке, а затем в точке М(1;1;1): grad u (М) = {2; 2; 2}.
Нормируем вектор 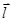 = {2;1;-2}.
= {2;1;-2}.
Для этого найдем его длину 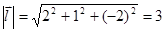 и координаты единичного вектора
и координаты единичного вектора 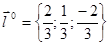 , где cosα = 2/3; cosβ= 1/3; cosγ = – 2/3/
, где cosα = 2/3; cosβ= 1/3; cosγ = – 2/3/
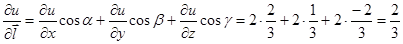 .
.
 2015-04-20
2015-04-20 1615
1615