Терема. Если в области D пространства R(3) задана непрерывная дифференцируемая функция u = u(x;y;z), определены в любой точке D
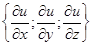 |
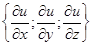 градиенты grad u (х;у; z) =, то производная по направлению вектора равна проекции градиента на его направление, то есть
градиенты grad u (х;у; z) =, то производная по направлению вектора равна проекции градиента на его направление, то есть 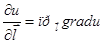 .
.
Действительно, так как 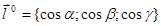 , grad u =, то
, grad u =, то 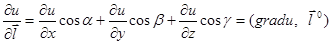 .
.
С другой стороны 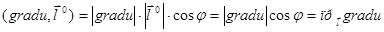 , где угол между градиентом grad u и вектором
, где угол между градиентом grad u и вектором 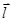 обозначен φ.
обозначен φ.
Следовательно, мы доказали, что 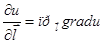 .
.
 2015-04-20
2015-04-20 424
424








