Рассмотрим, как располагаются значения δ r вокруг среднего значения. Для этого проведем серию замеров одной и той же величины и отобразим их результаты на таблице (Рис.2). Допустим, мы измеряем длину вала, номинальное (модельное) значение которой равно 100 мм. Возьмем листок бумаги «в клеточку» и в нижней его части проведем ось. Посередине поставим значение 100, а слева и справа последовательность значений с шагом 0,01 мм. Измерив значение величины, мы поставим крестик в клеточки над этим значением. Если результаты последующих измерений будут равняться тому же значению, крестик поставим клеточкой выше. Такой метод называется «Метод контрольных листков» [2] и широко применяется на практике при анализе причин появления некачественной продукции.
| Х | ||||||||||
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х | Х | ||||||||
| Х | Х | Х | Х | |||||||
| Х | Х | Х | Х | Х | Х | |||||
| Х | Х | Х | Х | Х | Х | Х | Х | Х | Х | |
| 99.95 | 99.96 | 99.97 | 99.98 | 99.99 | 100,01 | 100,02 | 100,03 | 100,04 | 100,05 |
Рис. 2. Контрольный листок
В нашем примере значение 99.99 встретилось 7 раз, 100,02 – 2 раза, а 100,05 ни разу.
Проделав достаточно большое число замеров, мы получим «горку». Изучив, таким образом, множество измерений совершенно различных величин, мы заметим, что форма «горки» (Рис. 3) оказывается схожей для всех них. Впервые дал этому математическое объяснение немецкий математик Гаусс. Но прежде чем рассказывать о его исследованиях нам придется познакомиться с основными понятиями теории вероятности. Вы будете подробно изучать этот курс. Поэтому сейчас мы остановимся только на некоторых, нужных для понимания метрологии, понятиях и фактах.
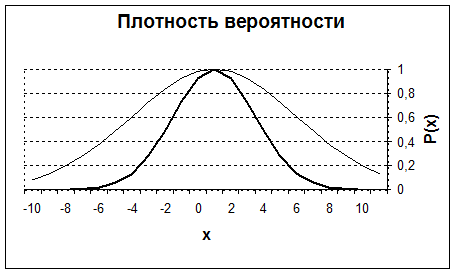
Рис. 3. Теоретические кривые Гаусса для различных распределений.
Назовем случайной величиной процесс, численную характеристику, которого нельзя предсказать заранее. Очевидно, многократное измерение одной величины является примером такого процесса. Частотой (N m) появления определенного значения (m) случайной величины назовем количество случаев, в которых случайная величина принимает данное значение. В нашем примере частота значения 99,99 равна 7. Если мы предполагаем, что частоты появления различных значений отражают свойства самой случайной величины, желательно выразить эти свойства вне зависимости от числа испытаний (в нашем примере, замеров). Назовем вероятностью того, что случайная величина примет данное значение, предел отношения:
P m= Lim (N m/N) (4)
N→ ∞
Где N m – частота появления значения m;
N – общее число испытаний.
Равенство полученного значения случайной величины определенному значению это событие в нашем вероятностном мире. Если события не зависят друг от друга, то вероятность появления какого - либо из них равна сумме их вероятностей[2]. Вероятность появления хоть какого-то события равна единице.
События, изображенные на рис. З находятся так близко друг от друга, что их можно представить в виде непрерывной последовательности. Тогда кривую, похожую на шляпу гнома, можно интерпретировать как плотность вероятности, показывающую, насколько изменится вероятность события, если величина изменится на единицу.
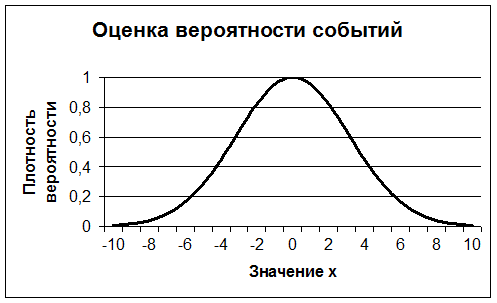
Вероятность события X < X0 будет равна площади под кривой, от линии X = X0 до -∞ (Рис. 4).
 | |||
 | |||
Рис 4. Оценка вероятности событий по графику функции плотности вероятности
Вероятность события X< -5 равна заштрихованной площади в левой части рисунка, вероятность X > 5, 5 равна заштрихованной площади в правой части рисунка.
Вся площадь под кривой – вероятность того, что Х примет хоть какое то значение равна единице. Тогда, вероятность того, что Х находится в интервале: X1<X<X2 равна единице минус заштрихованная площадь слева и справа. Выбрав X1 и X2 такими, чтобы заштрихованная площадь была небольшой (например, 0,01), мы можем сказать: «С доверительной вероятностью 1- 0,01= 0,99 величина X находится в интервале (X1; X2).
 2015-04-23
2015-04-23 522
522








