На практике часто приходится сталкиваться с ситуациями, в которых две или более стороны преследуют различные цели. Такие ситуации называются конфликтами. Математическая теория конфликтных ситуаций называется теорией игр.
Парной игрой с нулевой суммой называется игра, в которой участвуют два игрока (две стороны) причем, выигрыш одного игрока равен проигрышу другого. Каждый из игроков может применять стратегии, то есть совокупности определённых правил действий в зависимости от сложившейся ситуации. Если игрок А имеет m стратегий A1,…,Am, а игрок B – n стратегий B1,…,Bn, то говорят, что игра имеет размерность m×n.
Каждая пара стратегий (Ai, Bj) однозначно определяет исход игры, то есть выигрыш aij игрока A (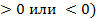 и проигрыш (- aij) игрока B.
и проигрыш (- aij) игрока B.
Матрица
P = 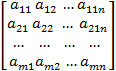
называется платежной матрицей игры.
Число 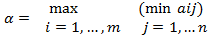
называется нижней ценой игры.
Число 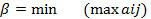
j=1,…n i=1,…,m
называется верхней ценой игры.
Если 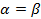 , то число ν =
, то число ν = 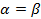 называется ценой игры.
называется ценой игры.
Пара стратегий (Ai, Bj), реализующая равенство нижней и верхней цены игры, называется седловой точкой игры и представляет собой пару оптимальных стратегий. В этом случае говорят, что игра решается в чистых стратегиях, поскольку на протяжении всей игры каждый игрок применяет только одну стратегию. Если игра не имеет седловой точки, то её оптимальное решение можно получить, случайным образом чередуя чистые стратегии.
Смешанной стратегией SA игрока А называется применение его чистых стратегий А1,…, Аmc вероятностями p1,…,pm, то есть
SA= 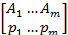 (
(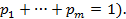
Аналогично определяется смешанная стратегия SB игрока B:
SB= 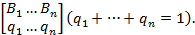
Вероятности pi или qjвыражают доли применения игроками A и B соответствующих чистых стратегий Ai или Bj.
Для нахождения оптимальных смешанных стратегий 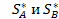 игроков А и В могут быть использованы аналитический и геометрический методы решения игры.
игроков А и В могут быть использованы аналитический и геометрический методы решения игры.
Рассмотрим игру разности 2×2 с платёжной матрицей
Р= 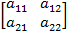 .
.
Если игра не имеет седловой точки, то её решение следует искать в смешанных стратегиях. Вероятности 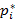 и
и 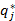 для оптимальных смешанных
для оптимальных смешанных
стратегий 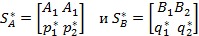 находятся из систем уравненений
находятся из систем уравненений
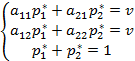 (4,1)
(4,1)
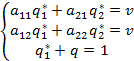 , (4,2)
, (4,2)
где ν – неизвестная цена игры. Рассмотренный метод решения игры называется аналитическим.
Геометрический метод решения базируется на принципах максимина и минимакса при определении нижней и верхней цены игры. На оси Оу и вертикальной прямой, пересекающей ось Ох в точке (1,0), откладываются отрезки, соответствующие элементам aij платёжной матрицы P. Для нахождения оптимальной стратегии 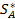 на оси Oу и вертикальной прямой откладываются значения
на оси Oу и вертикальной прямой откладываются значения 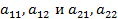 соответственно, а для нахождения оптимальной стратегии
соответственно, а для нахождения оптимальной стратегии 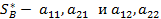 соответственно. Соединяя точки на этих прямых, как показано на рис. 4.1 и 4.2, находим точку пересечения наклонных отрезков.
соответственно. Соединяя точки на этих прямых, как показано на рис. 4.1 и 4.2, находим точку пересечения наклонных отрезков.


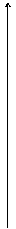 у y
у y

 a21 B11 a12
a21 B11 a12
 B2 a12 A2 a12 A1I
B2 a12 A2 a12 A1I




 М N
М N
B1 a11  B21 A1
B21 A1  A2I
A2I


 a22 a11 q2* q1*
a22 a11 q2* q1*
A1 v A2 х B1 v B2 x
Рис. 4.1 Pис.4.2
Из рис. 4.1 видно, что точка М имеет координаты 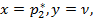 следовательно, может быть найдена оптимальная смешанная стратегия
следовательно, может быть найдена оптимальная смешанная стратегия 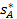 и цена игры
и цена игры 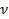 . Аналогично, в соответствии с рис. 4.2 точка N имеет координаты
. Аналогично, в соответствии с рис. 4.2 точка N имеет координаты 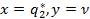 , а значит, можно найти оптимальную смешанную стратегию
, а значит, можно найти оптимальную смешанную стратегию 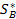 и цену игры
и цену игры 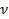 .
.
Пример 4.1.
Предприятие выпускает скоропортящуюся продукцию, которую можно сразу отправить потребителю (стратегия А1) или подвергнуть дополнительной обработке для длительного хранения (стратегия А2). Потребитель может немедленно приобрести продукцию (стратегия В1) или после длительного периода времени (стратегия В2), Проверить имеет ли данная игра 2×2 седловую точку и если нет, то найти решение игры в смешанных стратегиях. Матрица затрат (платёжная матрица) Р = 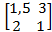 .
.
Решение.
Найдем нижнюю и верхнюю цены игры:
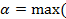 min(1,5;3); min(2;1))=max (1,5;1)=1,5,
min(1,5;3); min(2;1))=max (1,5;1)=1,5,
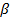 = min (max (1,5;2); max(3;1)) = min (2;3) =2
= min (max (1,5;2); max(3;1)) = min (2;3) =2
Поскольку 
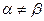 , то есть седловая точка отсутствует, необходимо искать решение игры в смешанных стратегиях. Будем искать оптимальную смешанную стратегию SA* =
, то есть седловая точка отсутствует, необходимо искать решение игры в смешанных стратегиях. Будем искать оптимальную смешанную стратегию SA* = 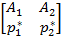 аналитическим методом.
аналитическим методом.
Согласно формуле (4.1) имеем
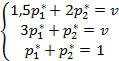 , (4.3)
, (4.3)
откуда p1*=  , p2*=
, p2*=  , v =
, v = 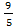 .
.
Таким образом, SA* = 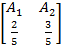 , а значит,
, а значит, 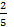 продукции следует сразу отправить потребителю а
продукции следует сразу отправить потребителю а 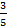 продукции подвергнуть дополнительной обработке. Оптимальную смешанную стратегию SB* =
продукции подвергнуть дополнительной обработке. Оптимальную смешанную стратегию SB* = 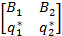 найдем геометрическим методом.
найдем геометрическим методом.
Построим декартову систему координат и выберем одинаковый масштаб на оси Оу и вертикальной прямой, проходящей через точку (1,0), после чего сделаем построение в соответствии с рис. 4.2.
 y
y
 A1I
A1I
 3
3


 A2 2 2
A2 2 2
A1 N
 q2* q1* A2ll 1
q2* q1* A2ll 1
B1 v B2 x
Рис.4.3
Из рис. 4.3. видно, что точка N(q2*,v) является точкой пересечения прямых A1 A1l и A2A2l, соответствующих стратегиях A1 и А2 игрока А. Используя вид уравнения прямой на плоскости, проходящей через две заданные точки, логично показать, что прямая А1 А11 проходящая через точки (0; 1,5) и (1; 3), удовлетворяет уравнению y=1,5x+1,5, а прямая 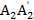 , проходящая через точки (0;2) и (1,1), удовлетворяет уравнению у= -х+2. Координата их точки пересечения N – это решение системы уравнений
, проходящая через точки (0;2) и (1,1), удовлетворяет уравнению у= -х+2. Координата их точки пересечения N – это решение системы уравнений
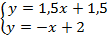 , (4.4)
, (4.4)
откуда 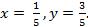
Имеем 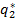 =
= 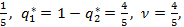 а значит,
а значит, 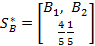 .
.
Таким образом, потребителю рекомендуется немедленно приобрести  продукции, а
продукции, а  продукции – после длительного периода времени.
продукции – после длительного периода времени.
 2015-04-20
2015-04-20 2759
2759
