Тема 5. Прогнозирование временных рядов

Временным (динамическим) рядом называется последовательность наблюдений некоторой переменной y в последующие моменты времени

t =1, 2, …, n.

Обычно модель временного ряда представляется в виде уравнения парной регрессии

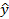_t= f(t), (5.1)

которое показывает, как в среднем меняется y в зависимости от t. Чаще всего временной ряд рассматривается в виде линейного тренда

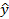_t= b₀ + b₁t. (5.2)

Коэффициент b_o и b₁ могут быть найдены с помощью метода наименьших квадратов по следующим формулам:

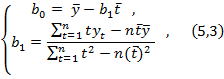
где n – число наблюдений переменных t и y,

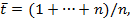
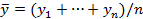
Используя временные ряды, можно осуществлять процедуру прогнозирования, которая представляет собой процесс построения умозаключений о будущем на основании имеющейся модели.

Существует два вида прогнозов: точечный и интервальный. Точечный прогноз представляет собой оценку значения прогнозируемой переменной и находится в результате подстановки в линейный тренд 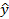_t=b₀+b₁t времени прогноза t = T. Интервальный прогноз представляет собой интервал, который с некоторой априорной вероятностью, называется достоверностью прогноза, содержит неизвестное значение прогнозируемой переменной.

Пусть T – время прогноза, тогда погрешность прогноза вычисляется по формуле:

S_T= 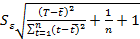, (5.4)

где S 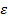– погрешность случайных отклонений, – временная средняя величина. При заданной достоверности прогноза 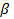по таблице функции Лапласа определяется соответствующий параметр 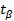. Истинное значение прогнозируемой переменной 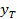с вероятностью 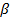располагается в интервале с центром в точечном прогнозе 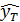, то есть

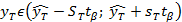
Пример 5.1.

Статистические данные о длине электрофицированных железнодорожных путей (тыс. км) представлены в таблице в виде временного ряда

Год
yt	3,9	4,0	4,4	4,7	5,1	5,6	6,0	6,3	6,5	6,7	6,9	7,1	7,4	7,8	8,3

Определить точечный и интервальный прогноз на длину таких путей на 1989 год, если достоверность прогноза 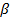= 0,95.

Решение:

По данным таблицы, используя метод наименьших квадратов, построим линейный тренд 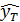= 3,581 + 0,382t. При этом считаем, что 1970 год соответствует t=1, 1971 год – t=2,… 1984 год – t=15, следовательно 1989 год соответствует t=T=20.

Найдем точечный прогноз: 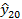= 3,581+0,38220=9,348 тыс.км. Погрешность случайных отклонений определяем по формуле:

,

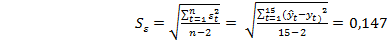откуда по формуле (5.4) погрешность прогноза

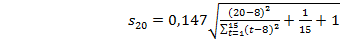=0,203 тыс. км.

Согласно таблице функции Лапласа при 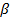= 0,95 имеем 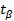= 1,96. Таким образом, интервальный прогноз представлен интервалом

(9,348-0,203 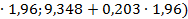= (9,745; 10,143).

Следовательно с вероятностью 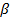=0,95 можно предположить, что в 1989 году длина электрофицированных железнодорожных путей будет находиться в этом интервале.