2015-04-23
345
Дифференциальным уравнением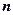 
- го порядка называется уравнение вида
.
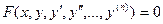Решением такого уравнения служит всякая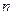 
раз дифференцируемая функция 
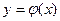, которая обращает данное уравнение в тождество, т.е.
.
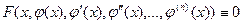Задача Коши для этого уравнения состоит в том, чтобы найти решение уравнения, удовлетворяющее условиям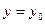 
, 
, …, 
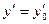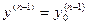при 
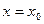,где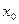 
, 
, 
, …, 
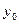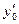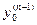- заданные числа, которые называются начальными данными, или начальными условиями.
Краевая задача для этого уравнения состоит в том, чтобы найти решение уравнения, удовлетворяющее граничным условиям. Эти условия (число которых не должно превышать порядка уравнения) задаются не в одной точке, а на концах некоторого промежутка.
Функция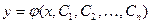 
называется общим решением данного дифференциального уравнения 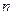- го порядка, если при соответствующем выборе произвольных постоянных 
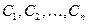эта функция является решением любой задачи Коши (краевой задачи), поставленной для данного уравнения.
Всякое решение, получаемое из общего решения при конкретных значениях постоянных 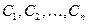, называется частным решением этого уравнения.
Линейным дифференциальным уравнением 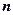- го порядка называется уравнение вида
.
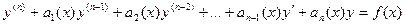Здесь функци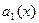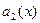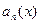и 
, 
, …, 
и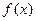 
заданы и непрерывны в некотором промежутке 
.
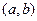Данное уравнение называется линейным неоднородным, или уравнением с правой частью. Если же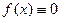 
, то уравнение называется линейным однородным. Однородное уравнениес той же левой частью, что и данное неоднородное, называется соответствующим ему.
