Линейным однородным дифференциальным уравнением 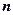 -го порядка с постоянными коэффициентами называется уравнение вида
-го порядка с постоянными коэффициентами называется уравнение вида
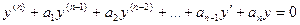 (2.1)
(2.1)
где коэффициенты 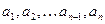 - некоторые действительные числа. Для нахождения частных решений уравнения (2.1) составляют характеристическое уравнение
- некоторые действительные числа. Для нахождения частных решений уравнения (2.1) составляют характеристическое уравнение
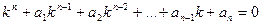 , (2.2)
, (2.2)
которое получается из уравнения (2.1) заменой в нем производных искомой функции соответствующими степенями 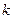 , причем сама функция заменяется единицей. Уравнение (2.2) является уравнением
, причем сама функция заменяется единицей. Уравнение (2.2) является уравнением 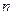 -й степени и имеет
-й степени и имеет 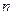 корней (действительных или комплексных, среди которых могут быть и равные).
корней (действительных или комплексных, среди которых могут быть и равные).
Тогда общее решение дифференциального уравнения (2.1) строится в зависимости от характера корней уравнения (2.2):
1) каждому действительному простому корню 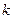 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 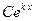 ;
;
2) каждому действительному корню кратности 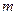 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 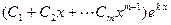 ;
;
3) каждой паре комплексных сопряженных простых корней 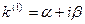 и
и 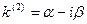 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 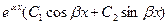 ;
;
4) каждой паре комплексных сопряженных корней 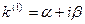 и
и 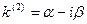 кратности
кратности 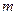 в общем решении соответствует слагаемое вида
в общем решении соответствует слагаемое вида 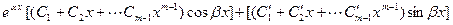 ;
;
 2015-04-23
2015-04-23 368
368








