Линейные однородные уравнения

Одним из замечательных свойств линейных уравнений является то, что общее решение таких уравнений можно найти по их известным частным решениям.

Теорема. Если 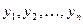- линейно независимые частные решения уравнения

,

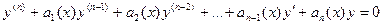то 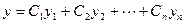есть общее решение этого уравнения ( 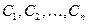- произвольные постоянные).

Примечание. Функции 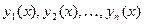называются линейно независимыми в промежутке 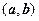, если они не связаны никаким тождеством

,

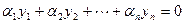где 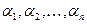- какие-нибудь постоянные, не равные нулю одновременно.

Для случая двух функций это условие можно сформулировать и так: две функци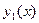и и 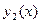линейно независимы, если их отношение не является постоянной величиной:

.

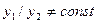Достаточным условием линейной независимости 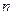функций, непрерывных вместе со своими производными до -го порядка в промежутке 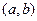, является то, что определитель Вронского (вронскиан) 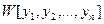этих функций не равен нулю ни в одной точке промежутка 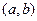, т.е.

.

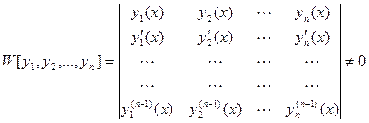Если данные 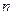функций являются частными решениями линейного однородного дифференциального уравнения 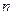- го порядка, то это условие (необращение в нуль) является не только достаточным, но и необходимым условием линейной независимости этих 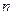решений.

Вронскиан 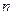решений линейного однородного дифференциального уравнения 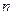- го порядка

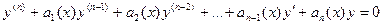
связан с первым коэффициентом этого уравнения 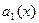формулой Лиувилля-Остроградского:

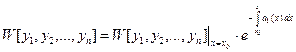
Совокупность 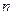решений линейного однородного дифференциального уравнения 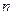- го порядка, определенных и линейно независимых в промежутке 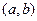, называется фундаментальной системой решений этого уравнения.

Для линейного однородного дифференциального уравнения второго порядка

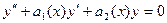
фундаментальная система состоит из двух линейно независимых решени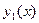й и 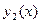; его общее решение находится по формуле

.

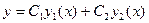Если для такого уравнения известно одно частное решение 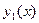, то второе его решение, линейно независимое с первым, можно найти по формуле (являющейся следствием формулы Лиувилля-Остроградского)

.

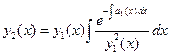Это дает возможность интегрировать линейные однородные уравнения второго порядка, для которых известно одно частное решение, сразу, не прибегая к понижению их порядка.