Рассмотрим как определяются кусочно-линейные базисные функции при решении одномерной задачи на отрезке 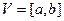 . Разобьем этот отрезок узлами
. Разобьем этот отрезок узлами 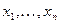 на конечные элементы
на конечные элементы 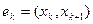 ,
, 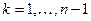 ,
, 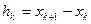 – длина
– длина 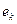 (шаг сетки). Каждому внутреннему узлу
(шаг сетки). Каждому внутреннему узлу 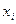 ставится в соответствие кусочно-линейная функция
ставится в соответствие кусочно-линейная функция 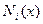
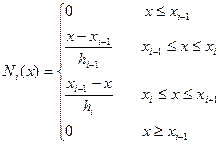
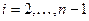 .
.
Для граничных узлов 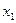 ,
, 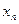 базисные функции имеют вид
базисные функции имеют вид
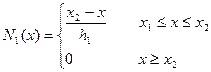 ,
, 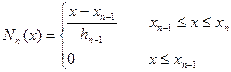 .
.
Базисные функции на элементе также называют функциями формы. Например, на рис. 1 представлены функции формы на отрезке  для равномерной сетки из трех элементов. Аппроксимируемая функция представляется в виде
для равномерной сетки из трех элементов. Аппроксимируемая функция представляется в виде 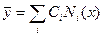 , где коэффициенты
, где коэффициенты 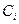 находятся из решения системы линейных алгебраических уравнений.
находятся из решения системы линейных алгебраических уравнений.
Важнейшими являются следующие свойства функции форм:
1. Функция 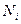 равна единице в узле
равна единице в узле 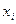 и нулю во всех других узлах.
и нулю во всех других узлах.
2. Функция 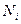 отлична от нуля только для элементов, содержащих узел
отлична от нуля только для элементов, содержащих узел 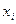 .
.
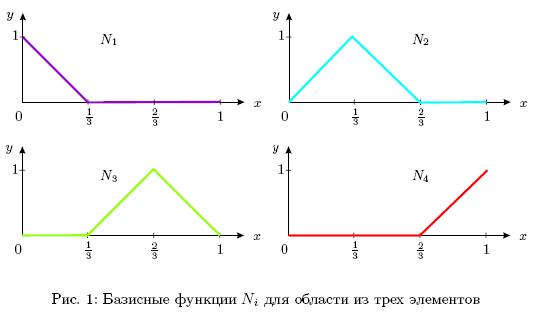
Выясним физический смысл коэффициентов 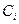 . Рассмотрим один конечный элемент
. Рассмотрим один конечный элемент 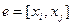 . На элементе
. На элементе 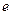 ненулевыми будут две базисные функции
ненулевыми будут две базисные функции 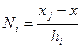 и
и 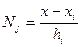 (см. рис. 2, пунктиром показаны части функции, лежащих вне элемента), поэтому
(см. рис. 2, пунктиром показаны части функции, лежащих вне элемента), поэтому
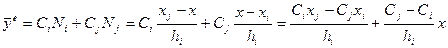 .
.
Решение должно удовлетворять уравнению в узлах, то есть 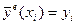 ,
, 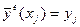 . Если подставить
. Если подставить 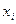 и
и 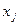 в выражение для
в выражение для 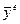 получим
получим 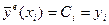 ,
, 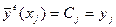 . То есть при таком выборе базисных функций, когда базисная функция равна единице в одном узле и нулю во всех других узлах, неизвестные коэффициенты
. То есть при таком выборе базисных функций, когда базисная функция равна единице в одном узле и нулю во всех других узлах, неизвестные коэффициенты 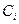 являются значениями функции в узлах
являются значениями функции в узлах 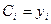 , то есть
, то есть 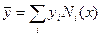 .
.
Пример
Решить краевую задачу методом конечных элементов
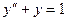
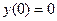 ,
, 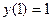 .
.
Прежде всего запишем интегральную формулировку для данного уравнения с помощью метода взвешенных невязок. Разбиваем отрезок на 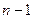 элементов с числом узлов
элементов с числом узлов 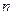 . Число базисных функций равно
. Число базисных функций равно 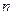 . Невязка
. Невязка
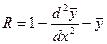 .
.
Запишем сначала условие равенства нулю невязки в общей форме
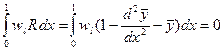
и, интегрируя по частям, понизим порядок производной под знаком интеграла
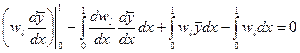 .
.
Понижение порядка дифференцирования под знаком интеграла – обычная процедура за счет которой можно ослабить требования на гладкость базисных функций. После интегрирования по частям от функций требуется только непрерывность базисных и весовых функций.
В методе взвешенных невязок весовая функция выбирается равной базисной 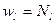 ,
, 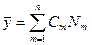 . В первом слагаемом заменять
. В первом слагаемом заменять 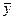 на сумму не будем (это слагаемое уйдет позже за счет граничных условий)
на сумму не будем (это слагаемое уйдет позже за счет граничных условий)
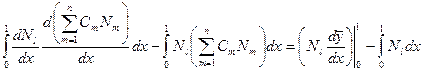 .
.
Кусочно-линейные базисные функции удовлетворяют требованию гладкости, так как они непрерывные. Слева выносим коэффициенты 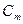 за знак интеграла. Получим
за знак интеграла. Получим
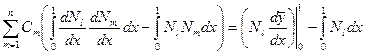 ,
,
где 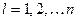 . Вводя обозначения
. Вводя обозначения
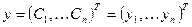 ,
,
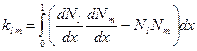 ,
, 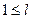 ,
,  ,
,
 ,
, 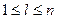 ,
,
получим систему линейных алгебраических уравнений
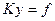 ,
, 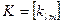 ,
, 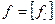 .
.
Заметим, что входящие в аппроксимирующие уравнения определенные интегралы могут быть получены простым суммированием их вклада по каждому элементу
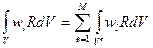 .
.
Вклад интеграла по элементу 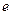 с узлами
с узлами 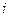 и
и 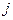 можно вычислить в общей форме. Причем формула для однотипных элементов будет одна и та же.
можно вычислить в общей форме. Причем формула для однотипных элементов будет одна и та же.
На элементе 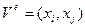 отличными от нуля функциями будут только функции
отличными от нуля функциями будут только функции 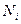 ,
, 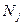 (рис. 2), то есть, если
(рис. 2), то есть, если  , то
, то 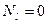 на
на 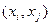 . Оценим вклад произвольного элемента в сумме
. Оценим вклад произвольного элемента в сумме 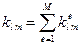 . Получим
. Получим
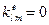 , если
, если 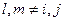 ,
,
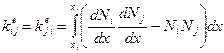 ,
,
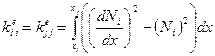 ,
,
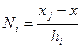 ,
, 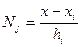 ,
, 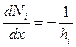 ,
, 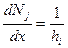 .
.
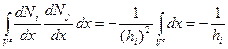 ,
, 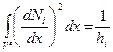 .
.
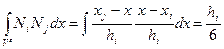 ,
, 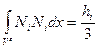 ,
,
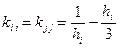 ,
, 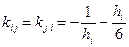 .
.
Элементная матрица для элемента 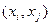 имеет вид
имеет вид
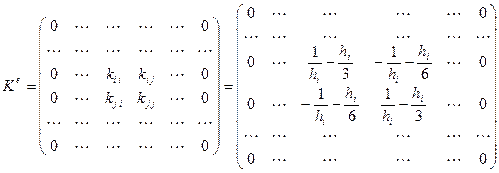
Вычислив компоненты матрицы элемента простым суммированием по всем элементам, получим матрицу 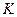 .
.
Процесс формирования глобальной матрицы системы 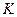 и глобального вектора правых частей в методе конечных элементов называется ансамблированием (или сборкой). Матрицу системы принято называть матрицей жесткости.
и глобального вектора правых частей в методе конечных элементов называется ансамблированием (или сборкой). Матрицу системы принято называть матрицей жесткости.
Запишем вид системы, например, для трех элементов и четырех узлов. Предположим, что все элементы имеют равную длину 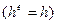 , тогда матрица жесткости приобретает вид
, тогда матрица жесткости приобретает вид
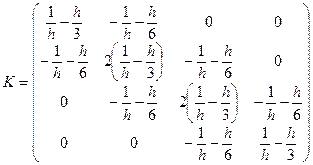 ,
, 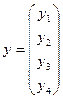 .
.
Вычислим вклад элемента 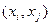 в вектор правых частей
в вектор правых частей 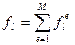 (отличными от нуля на элементе
(отличными от нуля на элементе 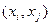 будут вклады при
будут вклады при 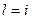 ,
, 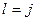 )
)
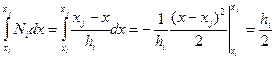 ,
,
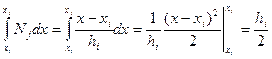 .
.
Заметим, что в точке  и
и 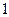 не равны нулю только базисные функции
не равны нулю только базисные функции 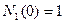 и
и 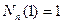 . Элементные векторы правых частей для первого элемента, для внутреннего элемента
. Элементные векторы правых частей для первого элемента, для внутреннего элемента 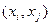
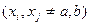 и для последнего элемента имеют вид (ненулевые значения стоят в позиции
и для последнего элемента имеют вид (ненулевые значения стоят в позиции 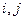 )
)
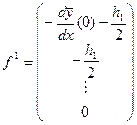 ,
, 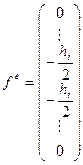 ,
, 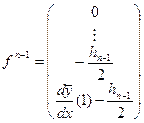 .
.
Для примера из трех элементов после сложения всех элементных векторов, получим глобальный вектор вида
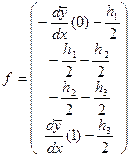 .
.
Значения производных в первом и последнем элементе вектора правых частей неизвестны, но далее вместо первого и последнего уравнений используем уравнения граничных условий 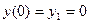 ,
, 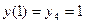 . Для симметричной матрицы системы граничные условия следует вносить следующим образом. Отметим, что до внесения граничных условий получаемая матрица системы вырождена.
. Для симметричной матрицы системы граничные условия следует вносить следующим образом. Отметим, что до внесения граничных условий получаемая матрица системы вырождена.
Учет граничных условий с сохранением симметрии матрицы системы.
Пусть в МКЭ получена СЛАУ 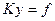 с симметричной матрицей
с симметричной матрицей 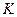 и необходимо учесть условие
и необходимо учесть условие 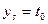 . Преобразование системы уравнений представляет собой двухшаговую процедуру. Пусть, например, известно значение
. Преобразование системы уравнений представляет собой двухшаговую процедуру. Пусть, например, известно значение 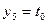 ; преобразование сводится тогда к следующему:
; преобразование сводится тогда к следующему:
1. Все коэффициенты пятой строки матрицы, за исключением диагонального, приравниваются к нулю 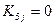 при
при 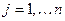 и
и  . Диагональный коэффициент приравнивается к единице
. Диагональный коэффициент приравнивается к единице 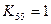 . Пятая компонента
. Пятая компонента 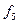 вектора
вектора 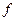 заменяется на значение
заменяется на значение 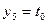 .
.
2. Из компонент вектора правых частей, кроме пятой компоненты, вычитается произведение пятого столбца матрицы на значение 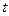 , затем пятый столбец матрицы (кроме диагонального элемента) обнуляется:
, затем пятый столбец матрицы (кроме диагонального элемента) обнуляется: 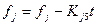 ,
, 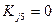 ,
,  ,
,  .
.
 2015-04-23
2015-04-23 1617
1617
