Проекционные методы решения краевых задач для обыкновенных дифференциальных уравнений

Краевыми задачами называются задачи, в которых дополнительные условия задаются при двух значениях независимой переменной (на концах рассматриваемого участка).

Рассмотрим краевую задачу на примере обыкновенного дифференциального уравнения второго порядка

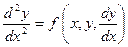
с граничными условиями

.

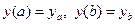Сущность проекционных методов состоит в разложении решения по базису некоторых функций (проекций)

.

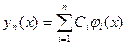Базис 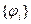выбирается в достаточной степени произвольно. В роли базисных функций могут выступать обычные полиномы 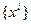, полиномы Лагранжа 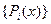, Фурье-гармоники, наборы синусов 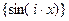и т.д.

Обязательные условия, которым должны удовлетворять базисные функции:

· разложение должно аппроксимировать ваше решение с любой, сколь угодно малой точностью (т.е. 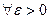существует такое 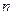, что норма отклонения );

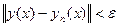· функции 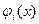должны быть линейно независимы;

· любая комбинация функций 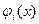должна удовлетворять поставленным граничным условиям.

После выбора базисных функций разложение подставляется в исходное уравнение, и получается система для расчета неизвестных коэффициентов .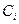

Недостатки проекционных методов:

· произвольность в выборе базиса (характер полученного решения в определенной степени определяется характером базисных функций);

· необходимость решения больших систем алгебраических уравнений.

Преимущества:

· решение находится сразу во всей области изменения независимой переменной, а не в отдельных точках;

· погрешность расчета одинакова во всем диапазоне изменения независимой переменной (отсутствует экспоненциальный рост погрешности, характерный для методов решения задачи Коши).