Метод Галеркина

Метод Галеркина используется для приближенного решения краевых задач для дифференциальных уравнений, как обыкновенных, так и в частных производных.

Рассмотрим краевую задачу

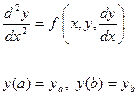(3.1)

Для ее приближенного решения выберем какую-либо последовательность базисных функций

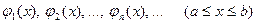(3.2)

т. е. последовательность функций, удовлетворяющих соответствующим однородным краевым условиям

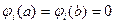
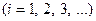
и обладающих свойством полноты. Последнее означает, что любую функцию из достаточно широкого класса, удовлетворяющую указанным однородным краевым условиям, можно разложить в ряд по функциям (3.2).

Чаще всего полагают

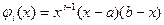или , .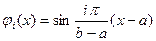

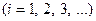Кроме того, надо выбрать какую-нибудь функцию 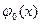, удовлетворяющую краевым условиям, указанным в (3.1), например,

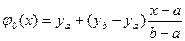или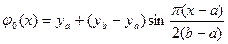

Приближенное решение задачи (3.1) ищется в виде

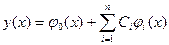, (3.3)

где функции 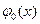, , 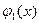… 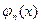мы задаем, а постоянные 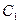, , 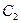…, 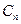подбираем. Тогда краевые условия, указанные в (3.1), заведомо удовлетворяются, а при подстановке выражения (3.3) в дифференциальное уравнение получается невязка (т. е. разность между левой и правой частями уравнения)

.

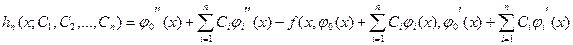С ее помощью получаем систему из 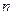уравнений с 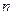неизвестными для определения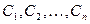

.

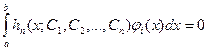
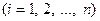3.2. Реализация метода Галеркина в|посредством| MathCad

Пример. Найти методом Галеркина приближенное решение краевой задачи

, .

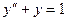
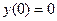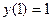Приведем решение краевой задачи с помощью|посредством| программного комплекса MathCad:

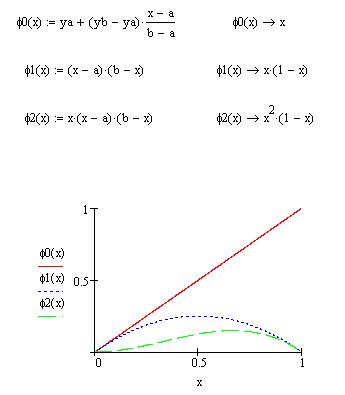
Сравним, значения точного и приближенного решений:

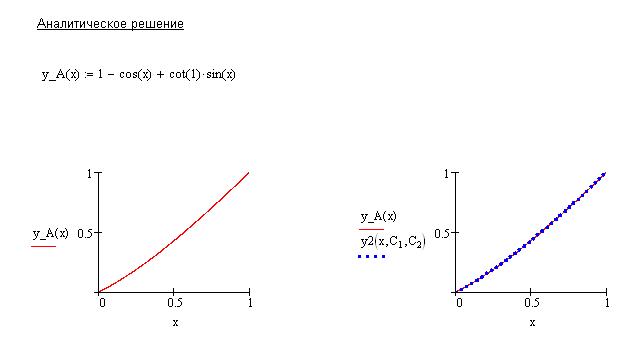
например, при 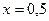имеем

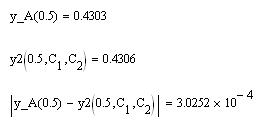
Как видим, погрешность близка к 0,03 %. Для получения более точного решения необходимо использовать большее количество базисных функций.