Алгоритм

1. Вычисляем координаты узлов:
Шаг сетки ;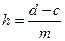
Для ;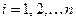

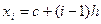2. В цикле по элементам: Для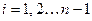

2.1 Формируем элементную матрицу .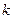

2.2 Проводим процесс сборки – формируем глобальную матрицу жесткости , , , .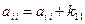

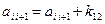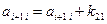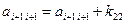2.3 Формируем элементный вектор правых частей .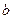

2.4 Проводим процесс сборки – формируем глобальный вектор правых частей , .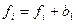

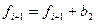3. Вносим граничное условие 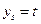в матрицу и вектор правых частей

3.1 ; ;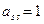

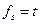3.2 Для ,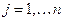
;
;

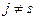
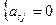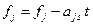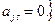
4 Решаем систему .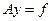

5 Выводим результат.

Приведем решение краевой задачи

, .

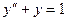
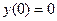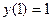с помощью|посредством| программного комплекса MathCad:

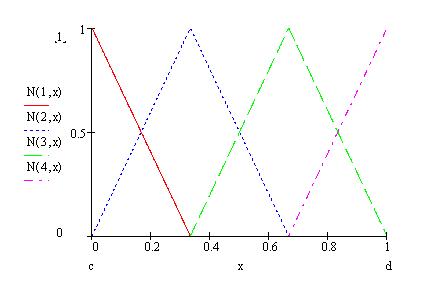
Сравним, значения точного и приближенного решений:

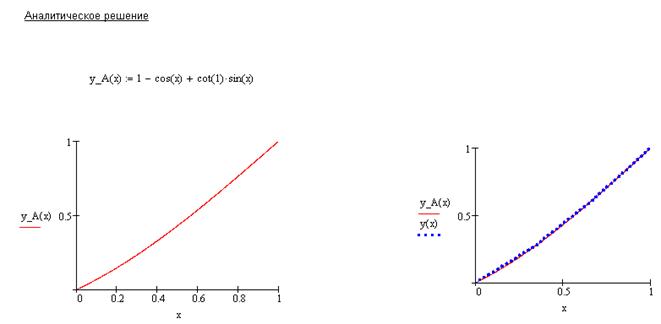
например, при 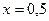имеем

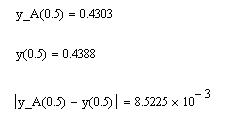
Как видим, погрешность близка к 0,85 %. Для получения более точного решения необходимо использовать большее количество базисных функций.

Варианты индивидуальных заданий

№ 1. Решить нелинейную систему уравнений методом Ньютона с точностью .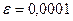

1)

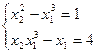
2)

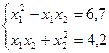
3)

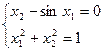
4)

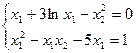
5)

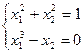
6)

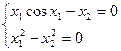
7)

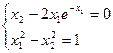
8)

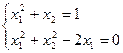
9)

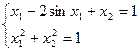
10)

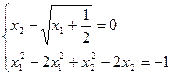
11)

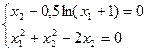
12)

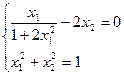
13)

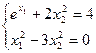
14)

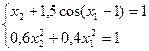
15)

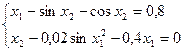
16)

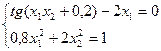
17)

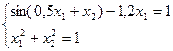
18)

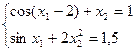
19)

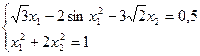
20)

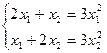
21)

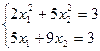
22)

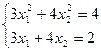
23)

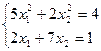
24)

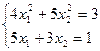
25)

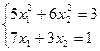
26)

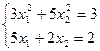
27)

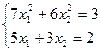
28)

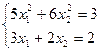
29)

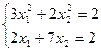
30)

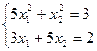
№ 2, №3. Решить краевую задачу методом Галеркина и методом конечных элементов

нечетные варианты: , ,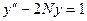

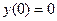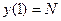четные варианты: , ,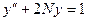

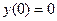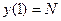где 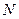- номер варианта.