Основные свойства и модели детерминированного факторного анализа

Моделирование – это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь передается в форме конкретного математического уравнения.

Основные свойства детерминированного подхода к анализу:

· определение детерминированной модели путем логического анализа;

· наличие полной (жесткой) связи между показателями;

· невозможность разделить результаты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;

· изучение взаимосвязей в краткосрочном периоде.

Детерминированный факторный анализ проводится по этапам:

1) построение экономически обоснованной детерминированной факторной модели;

2) выбор приема анализа и подготовка условий для его выполнения;

3) реализация счетных процедур;

4) формулирование выводов.

Детерминированные модели могут быть разного типа.

1. Аддитивные модели:

.

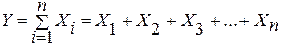Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.

2. Мультипликативные модели:

.

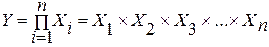Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.

3. Кратные модели:

.

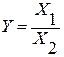Они применяются тогда, когда результативный показатель получают делением одного фактора на величину другого.

4. Смешанные (комбинированные) модели:

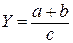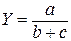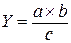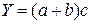; ; ; и т.д.

Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции можно применять такие детерминированные модели, как:

; ; ,

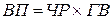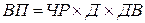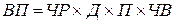где ВП – валовая продукция предприятия; ЧР численность работников предприятия; ГВ – среднегодовая выработка продукции одним работником; Д - количество отработанных дней одним рабочим за год; ДВ – среднедневная выработка продукции одним работником; П – средняя продолжительность рабочего дня; ЧВ – среднечасовая выработка продукции одним работником.

Аналогичным образом осуществляется моделирование аддитивных факторных систем за счет расчленения одного или нескольких факторных показателей на составные элементы.

Как известно, объем реализации продукции (VРП) равен:

VРП=VВП –VИ,

где VВП – объем производства; VИ - объем внутрихозяйственного использования продукции.

В хозяйстве продукция использовалась в качестве семян (С) и кормов (К), тогда приведенную исходную модель можно записать следующим образом: VРП=VВП –(С+К).

К классу кратных моделей применяют следующие методы их преобразования: удлинения, формального разложения, расширения и сокращения.

1. Метод удлинения факторной системы.

Исходная факторная модель 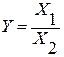. Если при этом

,

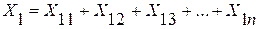Тогда модель примет вид:

.

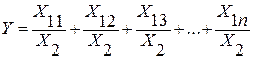2. Метод расширения факторной системы.

При использовании этого метода числитель и знаменатель умножаются на одно и то же число:

.

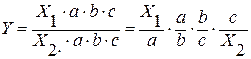3. Метод формального разложения факторной модели.

Данный метод предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей.

Если 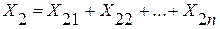, тогда

.

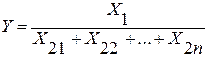4. Метод сокращения факторной модели.

При использовании этого метода числитель и знаменатель делятся на одно и то же число:

, , ,

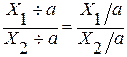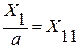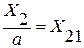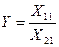
Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, поставленной цели, а также от профессиональных знаний и навыков исследователя.