Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае результат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния фактора на уровень результативного показателя. В этом его преимущество, а недостаток – в ограниченности сферы применения.
В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).
Математически этот метод описывается следующим образом. Допустим, что результативный показатель можно представить в виде произведения трех факторов: f =xyz. Прологарифмировав обе части равенства, получим
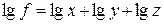 .
.
Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:
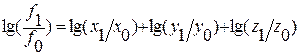 ;
;
или
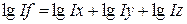 .
.
Разделив обе части равенства на lgIf и умножив на 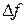 , получим:
, получим:
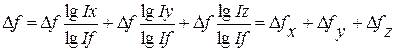 .
.
Отсюда влияние факторов определяется следующим образом:
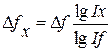 ;
; 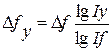 ;
; 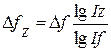 .
.
Используя данные табл. 6.1, вычислим прирост валовой продукции за счет численности рабочих (ЧР), количества отработанных дней одним рабочим за год (Д) и среднедневной выработки (ДВ) по факторной модели:
ВП = ЧР´Д´ДВ.
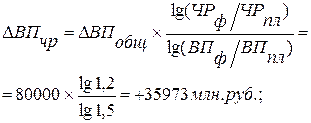
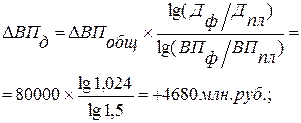
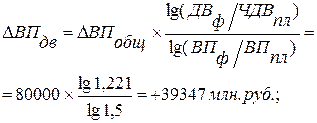
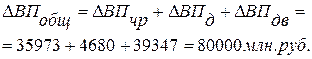
Сравнив полученные результаты расчета влияния факторов разными способами по данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов.
Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы:
| Прием | Модели | |||
| Мультипли-кативные | Аддитивные | Кратные | Смешанные | |
| Цепной подстановки | + | + | + | + |
| Индексный | + | - | + | - |
| Абсолютных разниц | + | - | - | Y = a(b – c) |
| Относительных разниц | + | - | - | Y = (a – b)c |
| Пропорционального деления (долевого участия) | - | + | - | Y = a/åxi |
| Интегральный | + | - | + | Y = a/åxi |
| Логарифмический | + | - | - | - |
Знание сущности данных приемов, области их применения, процедуры расчетов – необходимое условие квалифицированного проведения количественных исследований
 2015-04-23
2015-04-23 1484
1484







