Три способа описания движения материальной точки. Векторный способ. Определение скорости и ускорения

Теоретическая механика как наука. Три основных раздела ТМ. Кинематика. Основные задачи кинематики.

Теоретическая механика – наука об общих законах механических взаимодействий между материальными телами, а также об общих законах движения тел по отношению друг к другу.

Теоретическая механика, преподаваемая в техническом вузе, содержит три раздела: кинематику, статику и динамику:

Кинематика – часть механики, в которой изучаются зависимости между величинами, характеризующими состояние движения систем, но не рассматриваются причины, вызывающие изменение состояния движения.

Статика – это учение о равновесии совокупности тел некоторой системы отсчета.

Динамика – часть механики, в которой рассматривается влияние сил на состояние движения систем материальных объектов.

Основная задача кинематики заключается в установлении (при помощи тех или иных математических методов) способов задания движения точек или тел и в определении по уравнениям их движений соответствующих кинематических характеристик движения, таких, как траектории, скорости и ускорения движущихся точек, угловые скорости и угловые ускорения вращающихся тел и др.

Три способа описания движения материальной точки. Векторный способ. Определение скорости и ускорения.

Естественный способ. Этим способом пользуются, если из­вестна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве.

Координатный способ. Будем задавать положение точки с помощью координат. Если точка движется, то ее координаты изменяются с течением времени. Так как координаты точки зависят от времени, то можно сказать, что они являются функциями времени. В зависимости от формы траектории все движения точки делятся на прямолинейные и криволинейные. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая - криволинейным.

Математически это принято записывать в виде:

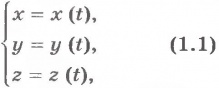
Векторный способ. Положение точки можно задать, как известно, и с помощью радиус-вектора. При движении материальной точки радиус-вектор, определяющий ее положение, с течением времени изменяется, т. е. является функцией времени: r=r(t) (стрелочки над ними нужны). Одна такая функция равняется трем функциям (1.1). Если ввести единичные векторы i, j, k (i = j = k = 1), направленные соответственно вдоль осей x, y и z то, очевидно, закон движения может быть представлен в виде:

r(t) = x(t)i + y(t)j + z(t)k.

Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности.