С развитием промышленности появились машины и станки, поэтому возникла необходимость изучить законы передачи движения между отдельными частями механизмов.
Так как исследование всего комплекса вопросов, связанных с взаимодействием сил в машинах и вызываемых этими силами движений, представляло весьма трудную задачу, то сперва решалась более простая задача, т. е. задача движения без учета сил, вызывающих это движение.
Все вопросы, связанные с движением без учета сил, вызывающих это движение, выделялись в особый раздел механики, названный Ампером кинематикой: «это — наука, в которой движения рассматриваются как таковые, которые мы наблюдаем в телах нас окружающих, и особенно в аппаратах, составляющих машины, которой я даю название кинематика» (А.М. Ampẻre. Essai sur la philosophic des siençes. 1835. Paris).
В 1862 г. вышел в свет «Трактат о чистой кинематике» Резаля. В этом сочинении вопросы прикладного характера были опущены. Резаль назвал свое сочинение чистой кинематикой в противовес кинематике Ампера, изучающей геометрию движения машин.
Таким образом, кинематикой стали называть раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения вне связи с силами, определяющими это движение.
Механическое движение непосредственно связано с понятиями «пространство» и «время». Это довольно сложные с философской, физической, любой другой точки зрения категории, которые в теоретической механике определяют с позиций механической (упрощенной) картины мира.
Пространств о – это бесконечная, трехмерная, однородная, изотропная протяженность, не зависящая ни от чего внешнего.
Время – это бесконечная, одномерная, однонаправленная, равномерная длительность, не зависящая ни от чего внешнего.
Положение любого исследуемого объекта (точки, тела) в пространстве всегда рассматривается по отношению к какому-либо другому объекту (телуотсчета ), которое условно считается неподвижным. В зависимости от постановки задачи за тело отсчета можно принять, например, Землю, фундамент машины, корпус судна и другие. Система координат, неизменно связанная с телом отсчета и снабженная часами для измерения времени, называется системойотсчета. Таким образом, в общем случае положение любой точки в выбранной системе отсчета характеризуется тремя геометрическими координатами (например, в декартовой системе – координаты х, у, z) и одной временной координатой – временем t.
Описать (или задать) движение точки – значит, по отношению к выбранной системе отсчета указать ее положение в любой момент времени. Для задания движения точки используют три основных способа: векторный, координатный и естественный.
Векторный способ. Задается векторное уравнение движения точки в виде векторной функции 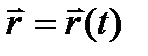 времени t, где
времени t, где 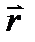 –радиус-вектор, проведенный из любой точки О тела отсчета в движущуюся точку М (рис. 4.1). Годограф радиус-вектора – геометрическое место последовательных положении конца радиус-вектора
–радиус-вектор, проведенный из любой точки О тела отсчета в движущуюся точку М (рис. 4.1). Годограф радиус-вектора – геометрическое место последовательных положении конца радиус-вектора 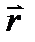 – представляет собой траекторию точки (линия АВ на рис. 10.1).
– представляет собой траекторию точки (линия АВ на рис. 10.1).
Координатный способ. В заранее выбранной, связанной с телом отсчета, системе прямоугольных координат задаются уравнения движения точки в координатной форме:
x=x(t), y=y(t), z=z(t),
где х, у, z – координаты движущейся точки М (рис. 3.1). Если точка движется в плоскости, ограничиваются двумя уравнениями, при движении по прямой – одним из трех уравнений движения. Эти же уравнения движения можно рассматривать как уравнения траектории АВ точки в параметрическом виде. Чтобы получить уравнение траектории точки в явном виде, если это возможно, следует из уравнений движения точки в координатной форме исключить параметр – время t.
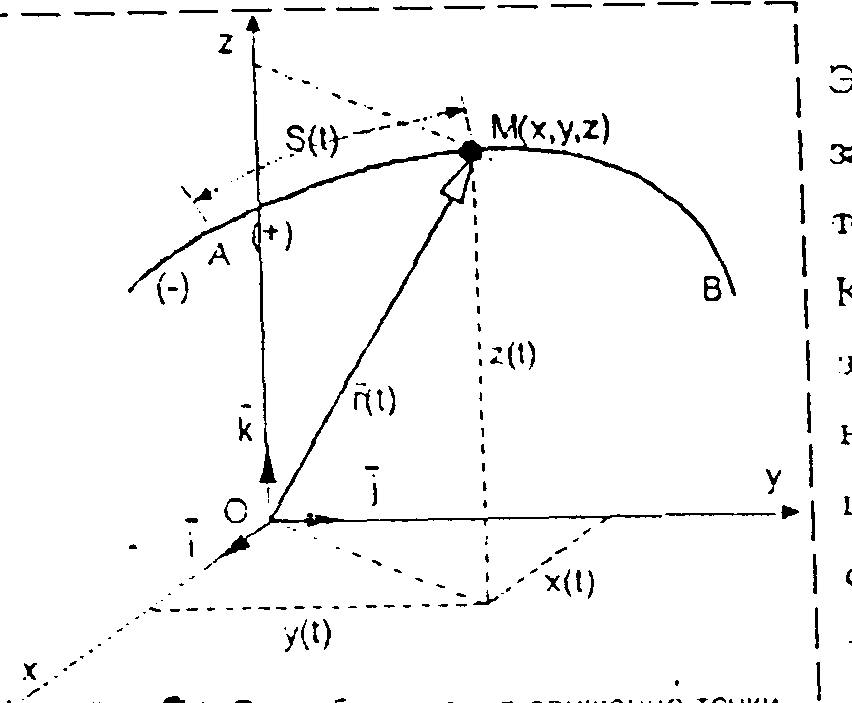
Рисунок 3.1 Способы задания движения точки
Естественный способ. Этот способ используют, когда заранее известна траектория точки (на рис. 3.1 – линия АВ). Кроме траектории точки, задают начало А и направление положительных соответственно, отсчета положительных (+) и, соответственно, отрицательных (-) дуговых координат S, определяющих положение точки М на траектории, а также закон или уравнение движения точки в естественнойформе как функцию дуговой координаты от времени: S = S (t). Следует различать расстояние AM по прямой, дуговую координату 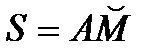 и путь, пройденный точкой за время t, – в общем случае они разные.
и путь, пройденный точкой за время t, – в общем случае они разные.
Все три способа взаимосвязаны между собой. Между векторным и координатным способами задания движения точки существует непосредственная связь: 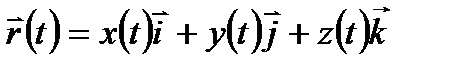 , где i, j, k – единичные векторы, направленные вдоль соответствующих осей координат х, у, z (рис. 4.1). Чтобы перейти от координатного к естественному способу, нужно сначала найти траекторию точки; начало отсчета дуговых координат обычно совмещают с начальным положением точки; направление отсчета положительных дуговых координат обычно совмещают с направлением движения точки. Уравнение движения в естественной форме получают из дифференциальной зависимости:
, где i, j, k – единичные векторы, направленные вдоль соответствующих осей координат х, у, z (рис. 4.1). Чтобы перейти от координатного к естественному способу, нужно сначала найти траекторию точки; начало отсчета дуговых координат обычно совмещают с начальным положением точки; направление отсчета положительных дуговых координат обычно совмещают с направлением движения точки. Уравнение движения в естественной форме получают из дифференциальной зависимости: 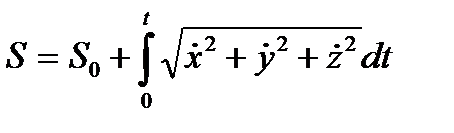 , где
, где 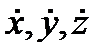 – производные по времени от координат х, у, z движущейся точки М (п. 10.1), S0 – начальная (при t = 0) дуговая координата точки. Обратный переход от естественного способа к координатному, (а затем и векторному) возможен, если заданная траектория точки (линия АВ на рис. 4.1) может быть описана аналитически. Тогда эту траекторию следует отнести к заранее выбранной прямоугольной системе координат xyz и из геометрических соотношений найти уравнения движения точки x=x(t),y=y(t), z=z(t).
– производные по времени от координат х, у, z движущейся точки М (п. 10.1), S0 – начальная (при t = 0) дуговая координата точки. Обратный переход от естественного способа к координатному, (а затем и векторному) возможен, если заданная траектория точки (линия АВ на рис. 4.1) может быть описана аналитически. Тогда эту траекторию следует отнести к заранее выбранной прямоугольной системе координат xyz и из геометрических соотношений найти уравнения движения точки x=x(t),y=y(t), z=z(t).
СКОРОСТЬ ТОЧКИ
Одной из кинематических характеристик точки является ее скорость.
Скорость точки – это физическая векторная величина, характеризующая быстроту изменения положения точки с течением времени. При анализе движения точки иногда находят ее среднюю скорость 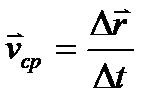 (здесь
(здесь 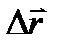 – приращение радиус-вектора точки за конечный промежуток времени
– приращение радиус-вектора точки за конечный промежуток времени 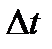 ), но важнее уметь находить мгновенную скорость (скорость точки в данный момент времени):
), но важнее уметь находить мгновенную скорость (скорость точки в данный момент времени): 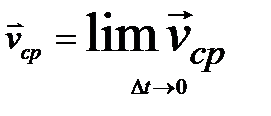 . Обычно скорость измеряют в м/с.
. Обычно скорость измеряют в м/с.
Если движение точки задано векторным способом, (мгновенная) скорость точки 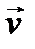 как вектор определяется производной по времени t от радиус-вектора
как вектор определяется производной по времени t от радиус-вектора 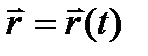 точки:
точки: 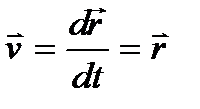 . При этом вектор скорости точки
. При этом вектор скорости точки 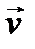 всегда направлен по касательной к траектории (рис. 3.2).
всегда направлен по касательной к траектории (рис. 3.2).
Если движение точки задано координатным способом, скорость точки находится по проекциям скорости на соответствующие оси координат:
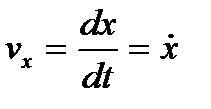 ,
, 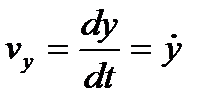 ,
, 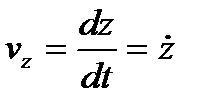 ,
,
модуль скорости: 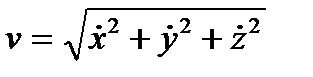 , а направление скорости определяется направляющими косинусами:
, а направление скорости определяется направляющими косинусами:
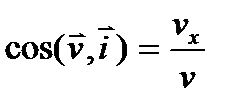 ,
, 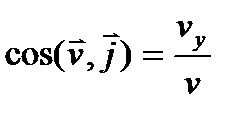 ,
, 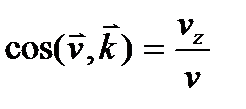 .
.
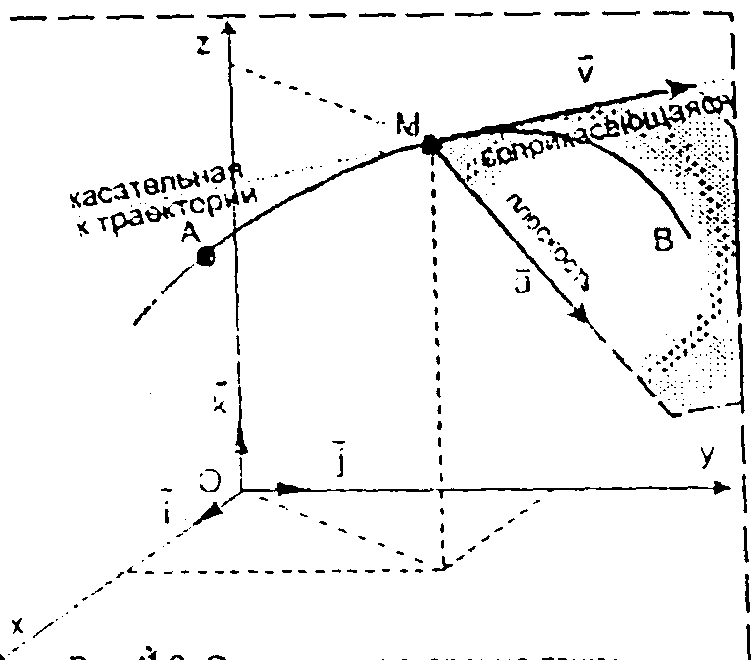
Рисунок 3.2 Скорость и ускорение точки
Если движение точки задано естественным способом, модуль скорости определяется производной по времени t от дуговой координаты S: 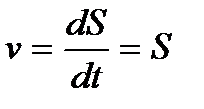 . Вектор скорости
. Вектор скорости 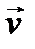 всегда направлен по касательной к траектории в сторону возрастания дуговой координаты, если модуль скорости положительный (v> 0), или в обратную сторону, если v < 0.
всегда направлен по касательной к траектории в сторону возрастания дуговой координаты, если модуль скорости положительный (v> 0), или в обратную сторону, если v < 0.
Из взаимосвязи между собой всех трех способов задания движения точки вытекает выражение вектора скорости 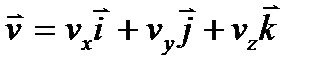 ,а также
,а также 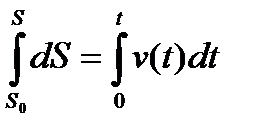 ,откуда после интегрирования приходим к известной уже дифференциальной зависимости.
,откуда после интегрирования приходим к известной уже дифференциальной зависимости.
Плоскопараллельным (или плоским ) называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных одной неподвижной (основной) плоскости.
Если координатную плоскость ху принять за основную (рис. 3.3, а), то окажется, что все отрезки, проведенные в теле перпендикулярно основной плоскости (например, на рис. 5.1, а отрезок CD – перпендикулярно плоскости ху), движутся поступательно. Следовательно, плоское движение тела можно рассматривать как движение одного любого его сечения, параллельного основной плоскости, а о плоскопараллельном движении тела можно говорить как о движении его плоского сечения (или плоской фигуры) в основной плоскости.
Для задания движения плоского сечения в основной плоскости (на рис. 3.3, б – сечения (S) в координатной плоскости ху) достаточно описать движение одной любой точки этого сечения, называемой полюсом (например, точки А на рис. 5.1, б), и добавить уравнение, описывающее вращение сечения в основной плоскости: 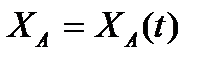 ,
, 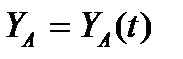 ,
, 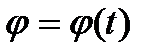 . Эти уравнения называются кинематическими уравнениями плоскопараллельного движения тела. Первые два из этих уравнений описывают поступательную часть плоского движения вместе с полюсом А, а третьеуравнение описывает вращение плоского сечения относительно оси, проходящей через полюс А перпендикулярно основной – плоскости. Суть плоскопараллельного движения в том, что его можно рассматривать каксовокупность одновременно происходящих простейших движений тела – поступательного вместе с полюсом и вращательного относительно полюса.
. Эти уравнения называются кинематическими уравнениями плоскопараллельного движения тела. Первые два из этих уравнений описывают поступательную часть плоского движения вместе с полюсом А, а третьеуравнение описывает вращение плоского сечения относительно оси, проходящей через полюс А перпендикулярно основной – плоскости. Суть плоскопараллельного движения в том, что его можно рассматривать каксовокупность одновременно происходящих простейших движений тела – поступательного вместе с полюсом и вращательного относительно полюса.
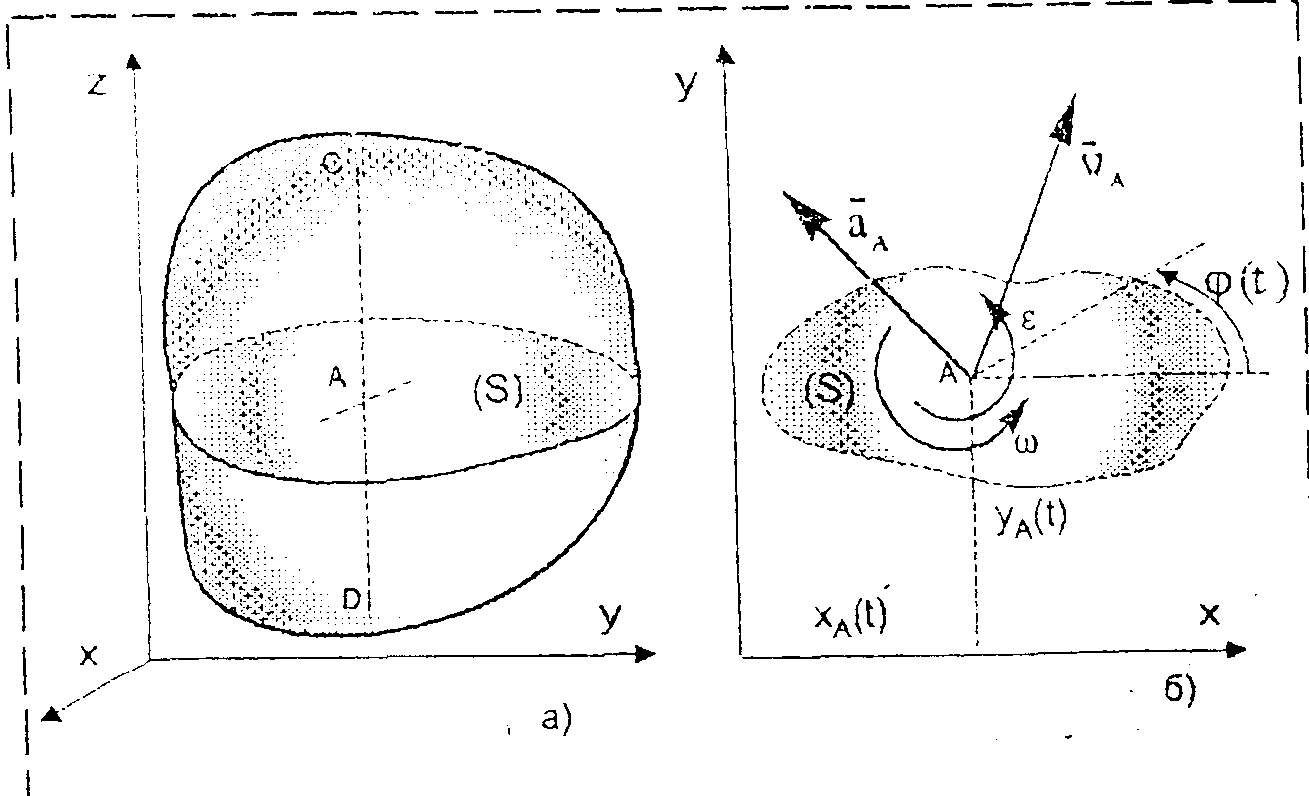
Рисунок 3.3. – Плоскопараллельное движение тела
По заданным кинематическим уравнениям плоскопараллельного движения можно найти (рис. 3.3, б): скорость 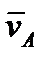 и ускорение
и ускорение 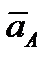 полюса 1), угловую скорость
полюса 1), угловую скорость 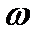 и угловое ускорение
и угловое ускорение 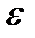 плоского сечения – основные кинематические характеристики плоского движения как совокупности кинематических характеристик простейших движений тела.
плоского сечения – основные кинематические характеристики плоского движения как совокупности кинематических характеристик простейших движений тела.
Свойства кинематических характеристик плоского движения: скорость 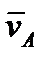 и ускорение
и ускорение 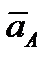 зависят, а угловая скорость
зависят, а угловая скорость 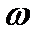 и угловое ускорение
и угловое ускорение 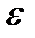 не зависят от выбора полюса А.
не зависят от выбора полюса А.
АБСОЛЮТНОЕ, ОТНОСИТЕЛЬНОЕ И ПЕРЕНОСНОЕ ДВИЖЕНИЯ
Обычно движение точки рассматривается по отношению к условно неподвижной системе отсчета (телу отсчета) или неподвижной системе координат xyz (п. 12.2). Иногда бывает удобным рассматривать движение точки в подвижной системе координат 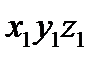 , которая в свою очередь движется в неподвижной системе координат xyz (рис. 3.3, табл. 3.1). В этом случае движение точки рассматривают как сложное или составное – такое, которое состоит из двух или более чем двух простых движений.
, которая в свою очередь движется в неподвижной системе координат xyz (рис. 3.3, табл. 3.1). В этом случае движение точки рассматривают как сложное или составное – такое, которое состоит из двух или более чем двух простых движений.
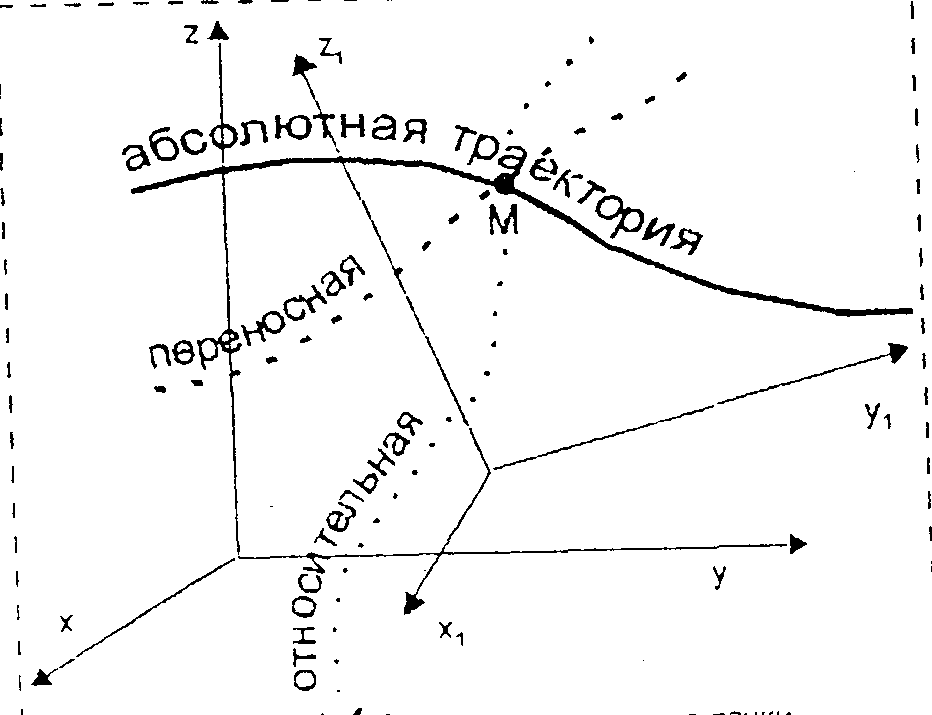
Рисунок 3.4 – Составное движение точки
Абсолютным называется движение точки по отношению к неподвижной системе координат xyz, которая связана с условно неподвижным телом. Траектория, скорость и ускорение точки в абсолютном движении называются соответственно абсолютной траекторией, абсолютной скоростью 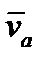 и абсолютным ускорением
и абсолютным ускорением 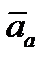 .
.
Относительным называется движение точки по отношению к подвижной системе координат 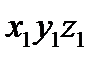 ,связанной с конкретным движущимся телом. Траектория, скорость и ускорение точки в относительном движении называются соответственно относительной траекторией, относительной скоростью
,связанной с конкретным движущимся телом. Траектория, скорость и ускорение точки в относительном движении называются соответственно относительной траекторией, относительной скоростью 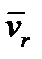 и относительным ускорением
и относительным ускорением 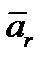 .
.
Переносным называется движение подвижной системы координат 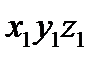 (движущегося тела) вместе с находящейся в ней движущейся точкой относительно неподвижной системы координат xyz. Траектория, скорость и ускорение той точки подвижной системы координат (подвижного тела), с которой совпадает в данный момент времени движущаяся точка, называются соответственно переносной траекторией, переносной скоростью
(движущегося тела) вместе с находящейся в ней движущейся точкой относительно неподвижной системы координат xyz. Траектория, скорость и ускорение той точки подвижной системы координат (подвижного тела), с которой совпадает в данный момент времени движущаяся точка, называются соответственно переносной траекторией, переносной скоростью 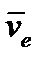 и переносным ускорением
и переносным ускорением 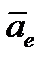 .
.
Совокупность приведенных выше определений, связанных с представлением о сложном движении точки, сведена в табл. 3.1.
Таблица 3.1. Представления о сложном движении точки
| Движение | Объект движения | Система отсчета | Пример |
| Абсолютное (а) | Точка М | Неподвижная система координат xyz | Человек относительно земли |
| Относительное (r) | Точка М | Подвижная система координат 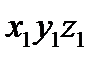 | Человек относительно движущегося поезда |
| Переносное (е) | Подвижная система координат 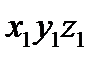 вместе движущейся в ней точки М вместе движущейся в ней точки М | Неподвижная система координат xyz | Поезд вместе с движущимся в нем человеком относительно земли |
ТЕОРЕМЫ О СЛОЖНОМ ДВИЖЕНИИ ТОЧКИ
Теорема сложения скоростей при сложном движении точки. Абсолютная скорость при сложном движении точки равна геометрической сумме относительной и переносной скоростей: 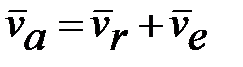 .
.
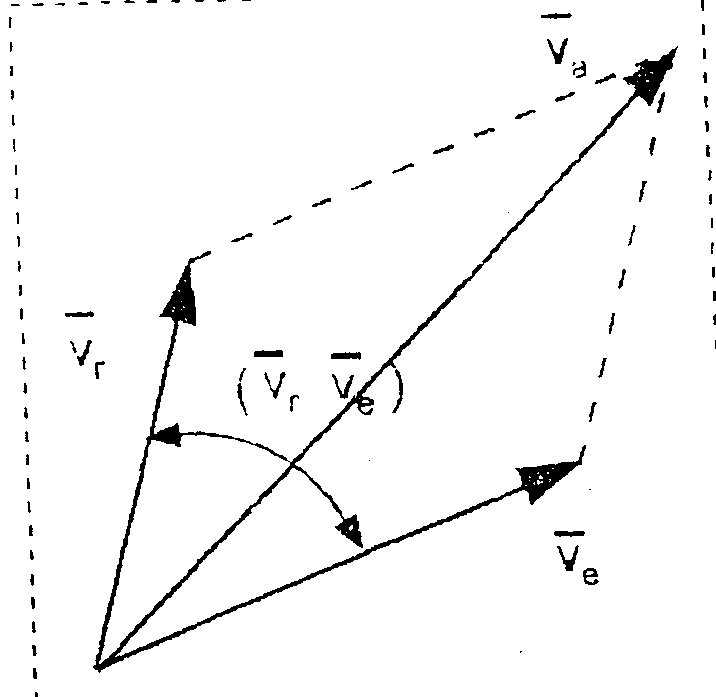
Рисунок 3.5 – Теорема сложения скоростей при сложном движении точки.
Если относительная и переносная скорости известны по модулю и направлению (рис. 3.5), модуль абсолютной скорости находят геометрически или аналитически способом проекций либо по теореме косинусов: 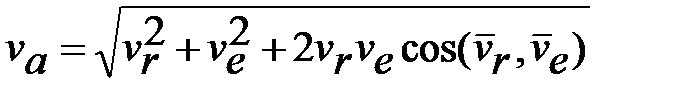 .
.
Теорема сложения ускорений при сложном движении точки (теорема Кориолиса). Абсолютное ускорение при сложном движении точки равно геометрической сумме относительного, переносного ускорений и ускорения Кориолиса: 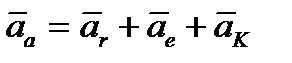 . Последняя составляющая
. Последняя составляющая 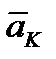 в этом векторном равенстве представляет собой ускорение Кориолиса (п. 13.3).
в этом векторном равенстве представляет собой ускорение Кориолиса (п. 13.3).
Учитывая, что в общем случае абсолютное, относительное и переносное ускорения раскладываются на касательные и нормальные составляющие, теорему Кориолиса при необходимости используют в развернутой форме: 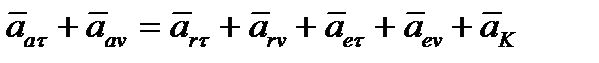 . Такие векторные равенства обычно решают графически или аналитически способом проекций, тогда модуль абсолютного ускорения:
. Такие векторные равенства обычно решают графически или аналитически способом проекций, тогда модуль абсолютного ускорения: 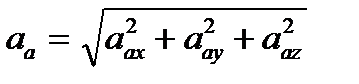 , где
, где 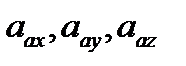 – проекции абсолютного ускорения на заранее выбранные оси координат.
– проекции абсолютного ускорения на заранее выбранные оси координат.
Литература: Яблонский А.А., Никифорова В.А.Курс теоретической механики. ч.1,2: Учебник. М., 1984. /1/ Глава 8. §66-68.
Вопросы для самопроверки и задания:
1. Какое движение называется плоским?
2. Кинематические уравнения плоскопараллельного движения.
3. От каких параметров зависят угловая скорость 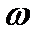 и угловое ускорение
и угловое ускорение 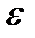 ?
?
4. Кинематика точки.
6. Приведите примеры простейшего вида движения.
7. Какие уравнения представляют с собой кинематические уравнения?
8. Что является основными кинематическими характеристиками поступательно движущегося тела?
9. Что называют абсолютным, относительным, переносным движением точки?
10. Какая связь существует между абсолютной, переносной и относительной скоростями точки?
 2015-06-05
2015-06-05 3920
3920








