2015-04-23
971
Исследовать ряд на сходимость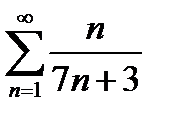 
.
Решение.
Замечание. При исследовании рядов на сходимость необходимо хорошо понимать, что такое предел и хорошо уметь раскрывать неопределенность типа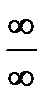 
.
При вычислении предела в качестве «динамической» переменной выступает n, а пределы с переменной «эн» – пределы числовых последовательностей. Отличие состоит в том, что переменная «эн» принимает дискретные (прерывные) натуральные значения: 1, 2, 3 и т.д. Но данный факт мало сказывается на методах решения пределов и способах раскрытия неопределенностей.
Итак, находим предел общего члена числового ряда: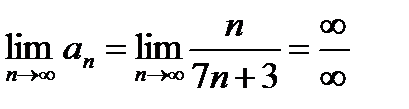 
Напоминаю, что при раскрытии неопределенности типа бесконечность, деленная на бесконечность числитель и знаменатель дроби делят на старшую степень переменной, в данном случае это n:
| бмф |
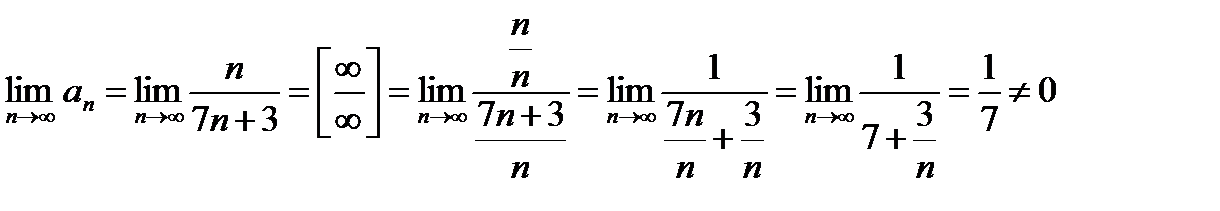
Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.
Пример
Исследовать ряд на сходимость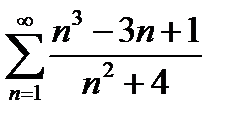 
Решение.
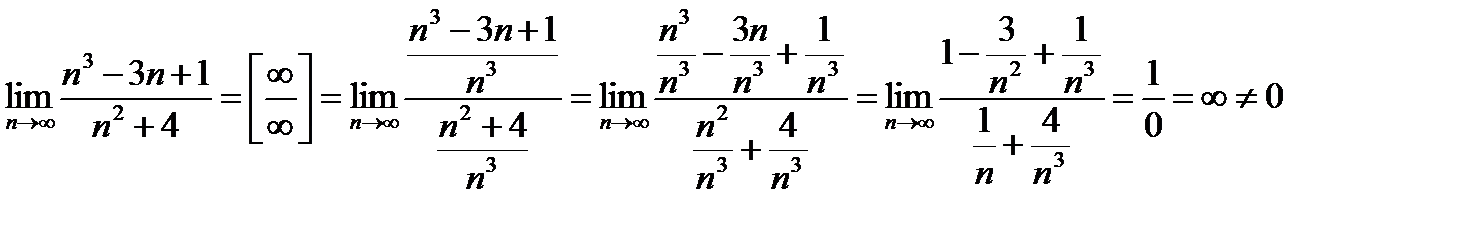
Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.
|
|
|
Необходимый признак сходимости не дает возможности судить о том, сходится ли данный ряд. Сходимость и расходимость ряда во многих случаях можно установить с помощью, так называемых достаточных признаков. Рассмотрим некоторые из них для знакоположительных рядов. (Так как умножение на всех членов ряда на число не влияет на его сходимость, знакоотрицательный ряд переходит в знакоположительный при умножении его на (-1)).
