Теорема 1. Если ряд 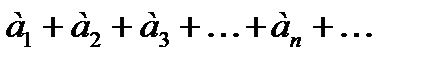 сходится и имеет сумму S, то ряд
сходится и имеет сумму S, то ряд 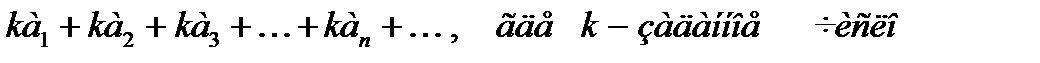 , также сходится и его сумма равна kS.
, также сходится и его сумма равна kS.
Теорема 2. Если ряды
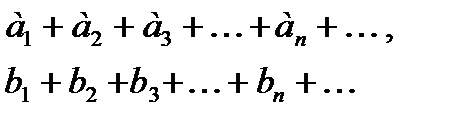
сходятся и имеют соответственно суммы S и S ¢, то ряд 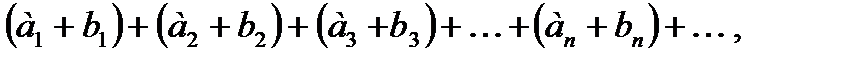 получающийся почленным сложением данных рядов, также сходится и имеет сумму S+S¢.
получающийся почленным сложением данных рядов, также сходится и имеет сумму S+S¢.
Теорема 3. Если сходится данный ряд, то сходится и ряд, полученный из данного отбрасыванием конечного числа k его первых членов. (Коротко, на сходимость ряда не влияет отбрасывание любого конечного числа его первых членов).
Пример
Найти сумму ряда 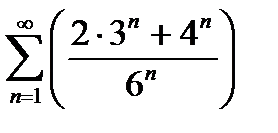
Решение.
Представим наш ряд в виде суммы двух рядов, пользуясь теоремами 1 и 2:
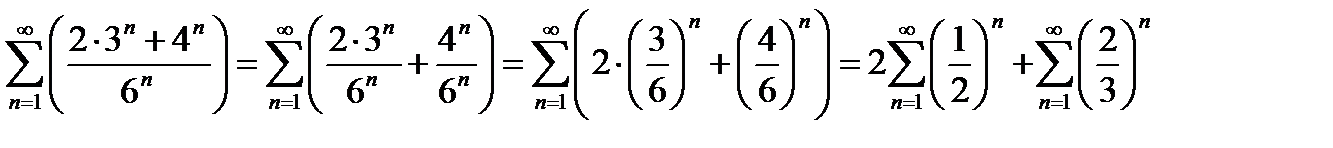
Оба ряда являются рядами геометрическими. Существенным является то обстоятельство, что речь идёт о сходящихся рядах. В данном примере мы заранее знаем, что обе геометрические прогрессии сойдутся, а значит, раскладываем исходный ряд в два ряда.
Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии:
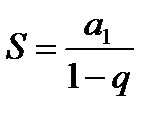 , где а1 – первый член прогрессии, q – знаменатель прогрессии.
, где а1 – первый член прогрессии, q – знаменатель прогрессии.
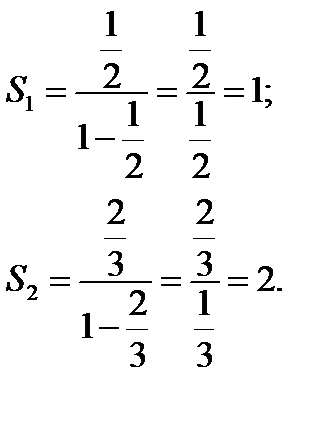
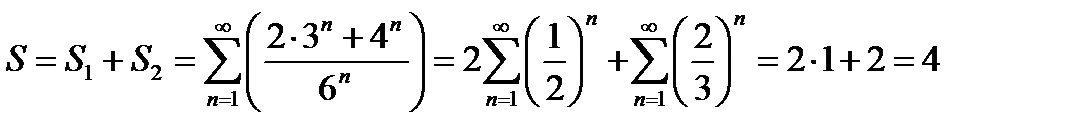 .
.
Итак, общий алгоритм исследования ряда на сходимость заключается в необходимости составления n -ой частичной суммы ряда Sn и нахождении предела 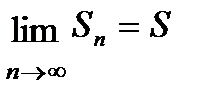 .
.
Пример
Исследовать ряд 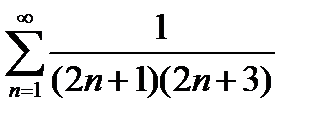 на сходимость.
на сходимость.
Решение.
На первом шаге нужно разложить общий член ряда в сумму дробей. Используем метод неопределённых коэффициентов:
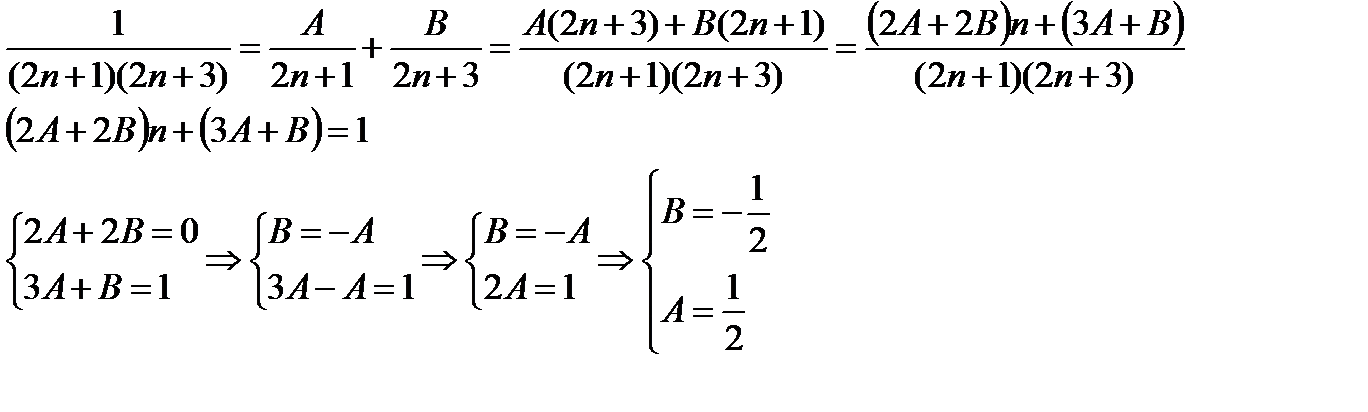
В результате: 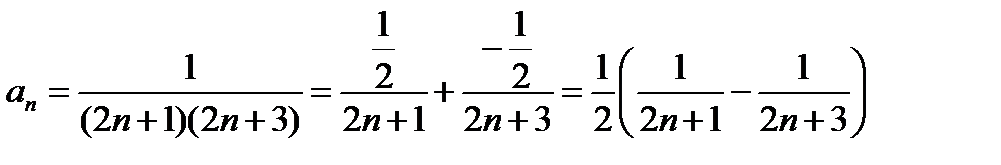
Составим частичную сумму ряда 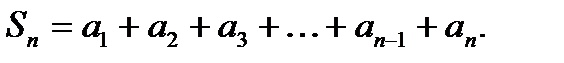
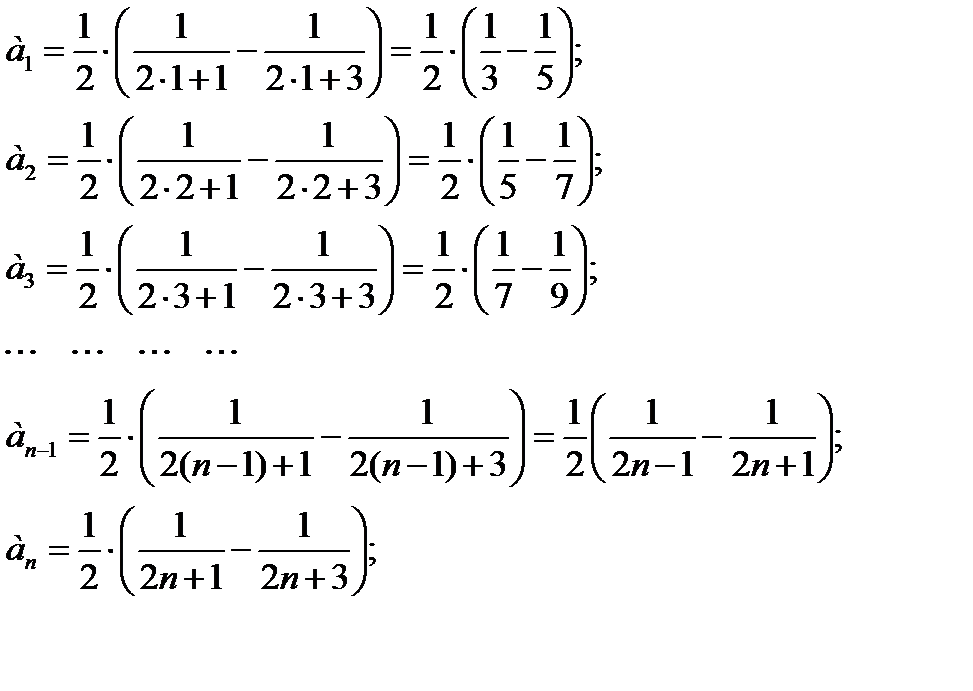
Почти все слагаемые частичной суммы благополучно сокращаются:
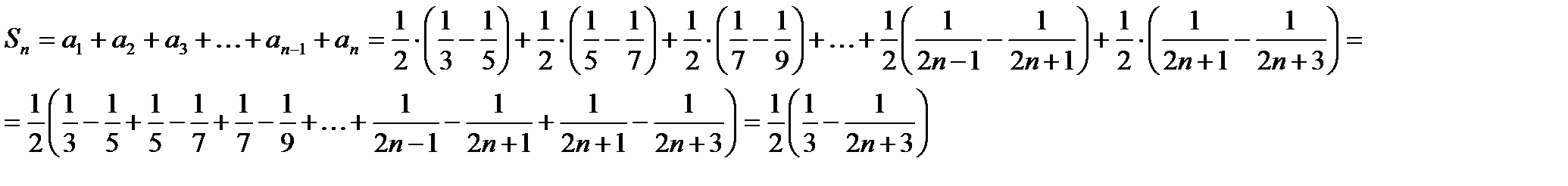
Осталось вычислить элементарный предел и узнать сумму ряда:
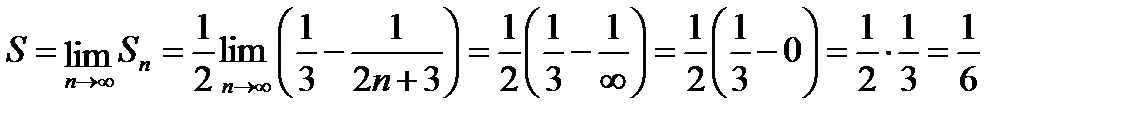 .
.
Предел частичных сумм ряда равен числу, т.е. конечен, следовательно, исходный ряд сходится.
В подавляющем большинстве случаев найти сумму ряда затруднительно, и поэтому на практике для исследования сходимости ряда используют специальные признаки, которые доказаны теоретически.
Существует несколько признаков сходимости ряда: необходимый признак сходимости ряда, признаки сравнения, признак Даламбера, признаки Коши, некоторые другие признаки. Когда какой признак применять? Это зависит от общего члена ряда 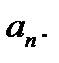
 2015-04-23
2015-04-23 2631
2631








