Проверка о распределении генеральной совокупности. Критерий Пирсона

Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения

Пусть имеется выборка, которой n, для проверки определенного закона распределения 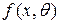с неизвестными параметрами .

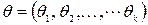Если рассматривается непрерывное распределение, то интервал возможных значений величины разбивается на m непересекающихся интервалов, в каждом из которых фиксируется число попаданий вариант выборки n₁, n₂,…, n_m.

Зная границы каждого интервала и принятый закон распределения, можно найти вероятность попадания случайной величины в этот интервал p_i. После этого из формулы 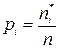находится теоретическая частота появления события : .

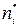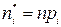В качестве критерия выбирается случайная величина

.

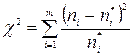Эта случайная величина при 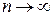стремится к закону распределения 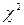с k степенями свободы.

Число степеней свободы определяется по формуле k=m-1-r, где m – число интервалов, r – число параметров предполагаемого распределения.

Так, для показательного распределения k=m-2, для нормального распределения k=m-3.

Далее, задавая уровень значимости a и учитывая k, из таблиц распределения 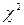находят критическое значение 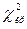, при котором выполняется условие

.

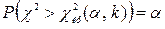Сравнивая вычисленное значение 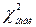со значением 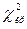, принимают решение о значимости допустимой гипотезы распределения случайной величины.

Пример. По полученным в результате измерений данным проверить гипотезу о нормальном распределении генеральной совокупности. В таблице указаны границы частичных интервалов и частоты попадания вариант в каждый интервал (n_i).