Сравнение двух дисперсий нормальных генеральных совокупностей

На практике часто требуется сравнить точность измерения различными приборами или методами.

Пусть имеются две нормально распределенные совокупност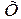и и 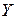. Так, например, если одну и ту же нормально распределенную случайную величину измеряют двумя приборами, то генеральные совокупности измеряемых значений будут разным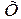и: и 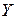. Из этих генеральных совокупностей извлекают выборки объемам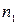и и 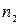и находят «исправленные выборочные значения 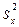и .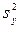

Зададим уровень значимости 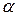. По данным значениям 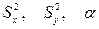проверим нулевую гипотезу, состоящую в том, что генеральные дисперсии равны: .

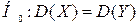«Исправленные» дисперсии являются несмещенными оценками генеральных дисперсий, т.е.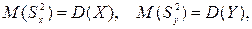

Поэтому .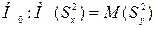

Таким образом, необходимо проверить равенство математических ожиданий «исправленных» выборочных дисперсий.

В качестве критерия проверки нулевой гипотезы примем отношение большей «исправленной» дисперсии к меньшей, т.е. случайную величину:

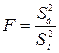
Величина 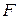имеет распределение Фишера-Снедекора со степенями свободы 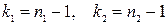, где 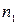- объем выборки большей «исправленной» дисперсии, 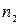- для меньшей.

Предположим, что большая дисперсия относится к измерениям 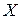, а меньшая - 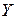. Тогда в качестве конкурирующей гипотезы можно принять

.

В этом случае критическую область находят из условия 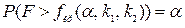(правосторонняя область).

Критическую точку находят по таблице распределения Фишера-Снедекора.

Пример. По двум независимым выборкам объемами n₁ =10, n₂ =15 найдены «исправленные» выборочные дисперсии 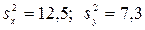. По уровню значимости 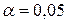проверить нулевую гипотезу .

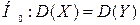Решение. Находим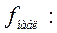

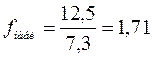
По таблице Фишера-Снедекора при 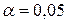, 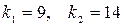находим 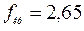. Так как 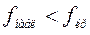, то нет оснований отвергать нулевую гипотезу.

В тех случаях, когда конкурирующая гипотеза может быть представлена в виде 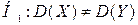, нужно строить двустороннюю критическую область и уровень значимости можно увеличить. При этом можно ограничиться нахождением правосторонней области для уровня значимости .

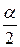Пример. По двум независимым выборкам объемами n₁ =10, n₂ =18 найдены «исправленные» выборочные дисперсии 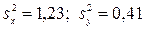. По уровню значимости 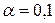проверить нулевую гипотезу 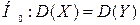при конкурирующей гипотезе .

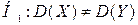Решение. Находим .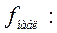

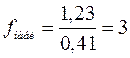Здесь критическая область двусторонняя, поэтому уровень значимости 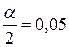, число степеней свободы 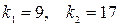. По таблице распределения Фишера находим критическую точку 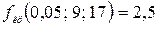. Так как 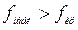, нулевую гипотезу отвергаем. Если при этом рассматривать два метода или прибора измерения, то предпочтительнее тот, у которого выборочная дисперсия меньше (т.е. 0,41)