Смешанное произведение 3х векторов равно объёму параллелепипеда, построенного на этих векторах, взятого со знаком + (-), если эти векторы образуют правую (левую) тройку.
Свойства:
1)смешанное произв не меняется при циклической перестановке его множителей.
(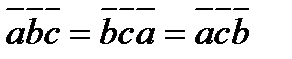 .
.
2)смешанное произв меняет знак при перемене мест любых букв любых сомножителей
3)смешанное произ ненулевых векторов =0 тога, когда они компланарны.
Смешанное произ векторов = определителю 3-его порядка, составленного из координат перемноженных векторов.
Приложение. 1)определение взаимных ориентаций векторов в пространстве: если 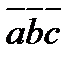 >0 (
>0 (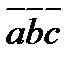 <0), то правая (левая) тройка векторов
<0), то правая (левая) тройка векторов 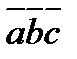
2)комплонарность векторов: 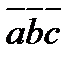 компланарны, когда их произв =0.
компланарны, когда их произв =0.
3)Геометрический смысл: Vпараллелепипеда= 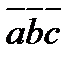 . Vтр=1/6(
. Vтр=1/6(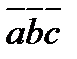 ).
).
Вычисление: 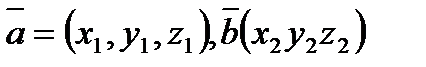 ,
, 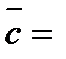
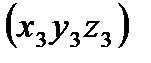
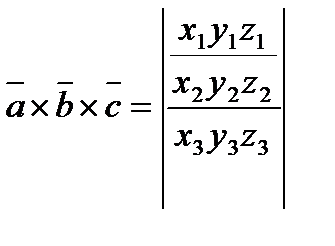
 2015-04-20
2015-04-20 665
665








