Эллипс

Геометрическое место точек, сумма расстояний от которых до двух фиксированных точек плоскости (обычно называемых фокусных) постоянна, называется эллипсом.

Если оси координат расположены так, что Ox проходит через фокусы F₁(C,0) и F₂(-C,0), а О(0,0) совпадает с серед отрезка F₁F₂, то по F₁М+F₂M получаем:

каноническое ур-ие эллипса ,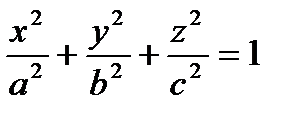

b²=-(с²-a²).

а и b- полуоси эллипса., а-большая, b-меньшая.

Эксцентриситет. 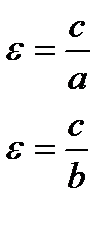, (если а>b)

(если а<b)

Эксцентриситет характеризует выпуклость эллипса.

У эллипса эксцентриситет находится: 0 .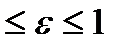

Случай 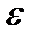=0 возникает только тогда, когда с=0, а это есть случай окружности – это эллипс с нулевым эксцентриситетом.

Директрисы (D) Геометрическое место точек, отношение расстояний от которых до точки эллипса к расстоянию от этой точки эллипса до фокуса постоянно и равно величине 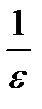, называется директрисами. .

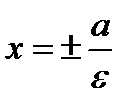Примечание: у окружности нет директрисы.