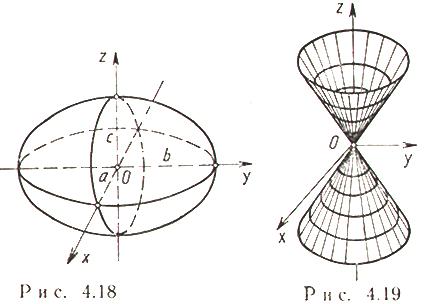
1. Исследуем поверхность 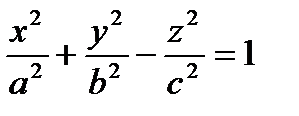 . Пересекая поверхностьплоскостью z=h, получим линию пересечения, уравнения которой имеет вид
. Пересекая поверхностьплоскостью z=h, получим линию пересечения, уравнения которой имеет вид
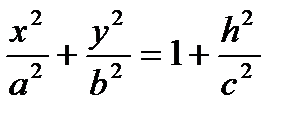
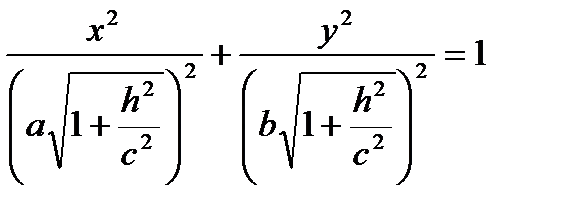
z=h. или z=h
полуоси: а1= 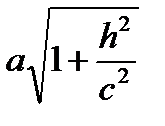 b1=
b1= 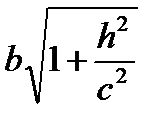
полуоси достигают своего наименьшего значения при h=0: а1=а, b1=b. При возрастании h полуоси эллипса будут увеличиваться. =>
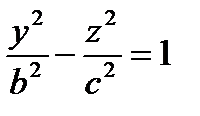
х=0.
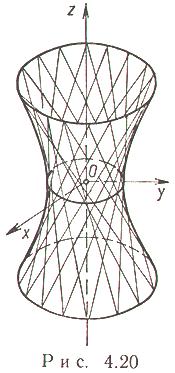
Анализ этих сечений показывает, что поверхность, определяемая уравнением, имеет форму бесконечной расширяющейся трубки. Поверхность называется однополостным гиперболоидом.
2. 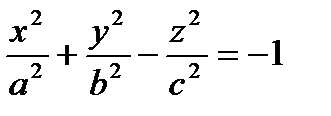 - уравнение поверхности.
- уравнение поверхности.
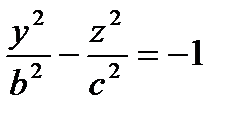 и
и 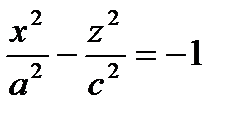 - поверхность, состоящая из 2 полостей, имеющих форму выпуклых неограниченных чаш. Поверхность называется двухполостным гиперболоидом.
- поверхность, состоящая из 2 полостей, имеющих форму выпуклых неограниченных чаш. Поверхность называется двухполостным гиперболоидом.
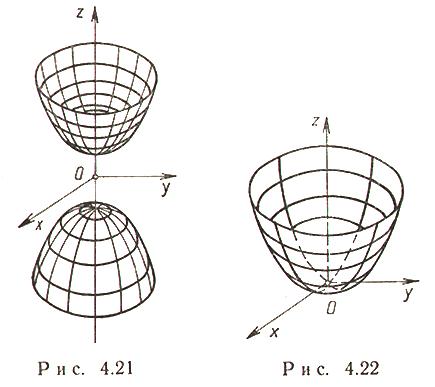
3. Конус второй степени
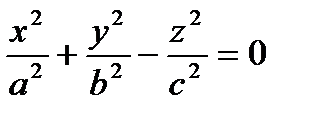
a = b - конус вращения (прямой круговой).
Сечения конуса плоскостями: в плоскости, пересекающей все прямолинейные образующие, - эллипс; в плоскости, параллельной одной прямолинейной образующей, - парабола; в плоскости, параллельной двум прямолинейным образующим, - гипербола; в плоскости, проходящей через вершину конуса, - пара пересекающихся прямых или точка (вершина).
26. Параболоид.
|
|
|
1.  -это эллиптический параболоид.
-это эллиптический параболоид.
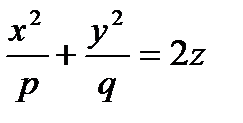 (р>0, q>0).
(р>0, q>0).
p = q - параболоид вращения вокруг оси Oz.
Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка.
2. 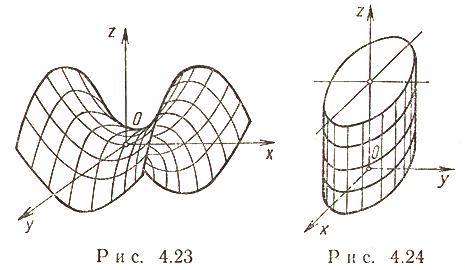 - гиперболический параболоид.
- гиперболический параболоид.
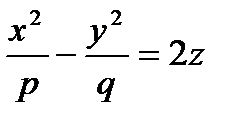
Сечения гиперболического параболоида плоскостями - либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).
 2015-04-20
2015-04-20 1203
1203