2015-04-20
1201
Геометрическое место точек, модуль разности расстояний от которых до двух фиксированных точек плоскости постоянна, называется гиперболой.
Каноническое уравнение гиперболы:
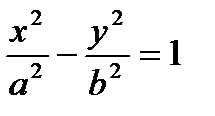, где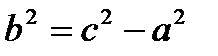 
.
Гипербола есть линия второго порядка.
Гипербола имеет 2 асимптоты: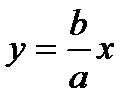 
и 
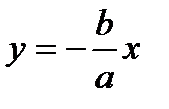
Гипербола называется равносторонней, если ее полуоси равны. (а=b). Каноническое уравнение:
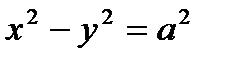
Эксцентриситет – отношение расстояния между фокусами к величине действительной оси гиперболы:
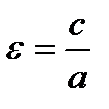
Так как для гиперболы с>а, то эксцентриситет гиперболы >1.
Эксцентриситет характеризует форму гиперболы: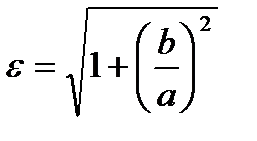 
. Эксцентриситет равносторонней гиперболы равен равен 
.
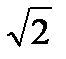Директрисы – прямые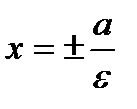 
.
Фокальные радиусы: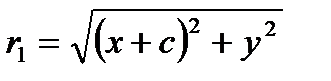 
и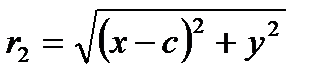 
.
Есть гиперболы, которые имеют общие асимптоты. Такие гиперболы называются сопряженными.
