Постановка задачи. На отрезке 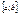 задано равномерное разбиение
задано равномерное разбиение 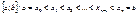 т.е дана система равноудаленных точек
т.е дана система равноудаленных точек 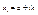 ;
; 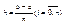 ;
; 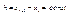 в этих точках известны значения функции
в этих точках известны значения функции 
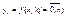 , вообще говоря сама функция неизвестна. По этим данным требуется построить полином степени не более чем n 1) degre
, вообще говоря сама функция неизвестна. По этим данным требуется построить полином степени не более чем n 1) degre 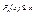 который в узлах принимает те же значения, что и сама функция 2)
который в узлах принимает те же значения, что и сама функция 2) 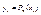
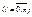 решение задачи 1)-2) будем искать в следующем виде
решение задачи 1)-2) будем искать в следующем виде 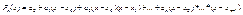 (6)где
(6)где 
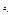 - пока неизвестные коэффициенты. Неизвестные коэффициенты
- пока неизвестные коэффициенты. Неизвестные коэффициенты 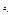 будем определять из условия 2) последовательно подстовляя в (6) в узловые точки
будем определять из условия 2) последовательно подстовляя в (6) в узловые точки 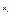 .
. 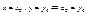
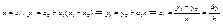
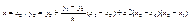 учитывая, что узлы равноудалены
учитывая, что узлы равноудалены 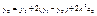
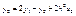
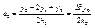
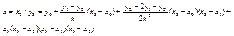
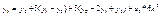
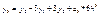
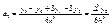

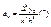 Подставим
Подставим 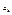 в (6)
в (6) 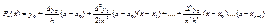
Этой формулы можно предать более компактный вид или ввести рассмотрение переменную q 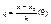
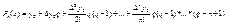 (10) где
(10) где 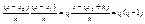 формула (10) является предпочтительной когда вычисления проводятся вручную
формула (10) является предпочтительной когда вычисления проводятся вручную
Замечание №1 Если 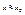 (близко с порцией точности), то
(близко с порцией точности), то 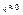 , в таких случаях в формуле (10) можно пренебречь слагаемыми, содержащими
, в таких случаях в формуле (10) можно пренебречь слагаемыми, содержащими 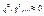 , тогда можно пользоваться
, тогда можно пользоваться 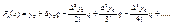 (11)
(11)
Замечание №2: первое ИПН обычно используется для приближенных значениях вычисления функции в начале таблице в первой половине.
Вопрос 17. II интерполяционный полином Ньютона. т.е задача с условиями 1)-2)
Решение задачи будем искать в следующем виде 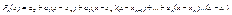 (12) где
(12) где 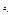 - пока еще неизвестный коэффициент. Неизвестный коэффициент будем определять из условия (2) последнее подставляем в (12) узловые точки, но не сначала, а с конца.
- пока еще неизвестный коэффициент. Неизвестный коэффициент будем определять из условия (2) последнее подставляем в (12) узловые точки, но не сначала, а с конца.
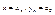
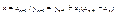
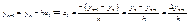
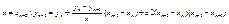
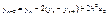
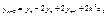
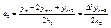
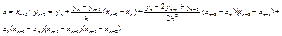
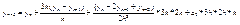
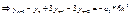
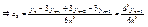

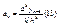 подставим (13) в (12) имеем следующие
подставим (13) в (12) имеем следующие 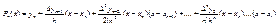 (14) по аналогии с предыдущими в ведем
(14) по аналогии с предыдущими в ведем 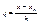 (15)
(15) 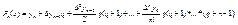 (16) где
(16) где 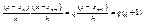
Замечание №3: Если 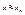 , то
, то 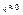 , поэтому можно пренебречь слагаемыми, содержащие,
, поэтому можно пренебречь слагаемыми, содержащие, 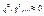 , тогда можно пользоваться
, тогда можно пользоваться 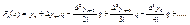 (17)
(17)
Замечание №4 Обычно 2-ой ИПН принимают для приближенных вычислений значения функции в конце таблицы.
Полиномы определяются единственным образом 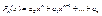 - стандартный вид полинома.
- стандартный вид полинома.
Погрешность приближения функции ИПН. Для оценки погрешности метода использована теорема 2. согласна этой теоремы 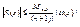
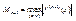
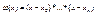
 2015-04-20
2015-04-20 545
545








