
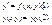 Задача1)-2). Заменим эту задачу эквивалентным интегральным уравнением.
Задача1)-2). Заменим эту задачу эквивалентным интегральным уравнением. 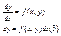 проинтегрируем обе части уравнения
проинтегрируем обе части уравнения 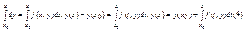 С учетом условия (2) уравнение (4) примет вид
С учетом условия (2) уравнение (4) примет вид 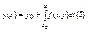 Задачу 1)-2) заменим эквивалентным интегральным уравнением(5)
Задачу 1)-2) заменим эквивалентным интегральным уравнением(5)
Доказательство 1)-2)=>(5) переход доказали Обратный переход (5) =>1)-2) 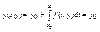 Продиффиринциируем (5)
Продиффиринциируем (5) 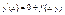 Интегрирование уравнения (5) решим методом последовательных приближений. y0-начальное приближение. y0 подставим в правую часть уравнения(5)
Интегрирование уравнения (5) решим методом последовательных приближений. y0-начальное приближение. y0 подставим в правую часть уравнения(5) 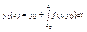 Полученное приближение подставим в правую часть уравнения (5)
Полученное приближение подставим в правую часть уравнения (5) 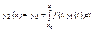
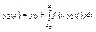 Произвольное n-ое приближение
Произвольное n-ое приближение 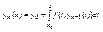 (6) n=1,2,3… Получим последовательность функций
(6) n=1,2,3… Получим последовательность функций 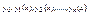 1)Сходится ли последовательность
1)Сходится ли последовательность
2) Чему равен 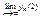
3) 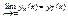 (
(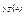 - точное решение) Равен ли предел последовательности точному решению задачи. Теорема 1 Если функция f(x,y)непрерывна по обеим переменным, существует ограниченная частная по y в рассматриваемой произвольной области, то
- точное решение) Равен ли предел последовательности точному решению задачи. Теорема 1 Если функция f(x,y)непрерывна по обеим переменным, существует ограниченная частная по y в рассматриваемой произвольной области, то 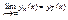
Как отличается полученное 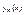 от
от 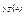 ?
?
Теорема 2 При выполнении условия теоремы 1 имеет место неравенство. 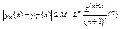 М- максимальное значение модуля функции в области G
М- максимальное значение модуля функции в области G 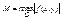 L- константа Липница.
L- константа Липница. 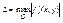
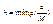 где c,d- границы области G
где c,d- границы области G 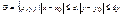 декартово произведение отрезков В области G должны выполнятся условия теоремы 1. Поясним область G
декартово произведение отрезков В области G должны выполнятся условия теоремы 1. Поясним область G 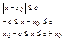
 2015-04-20
2015-04-20 765
765








