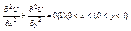Вопрос 39. Задача Дирихле для уравнения Лапласа

l- сторона квадрата, известна. В задаче Дирихле ставится граничное условие граничное условие 1-го рода. 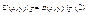где 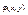- известная функция

Двумерную область покроем сеткой [0;l] 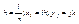Граница представляет собой квадрат. Произвольные внутренние узловые точки заменим. Для аппроксимации производных 2-го порядка используем формулы центральной разности 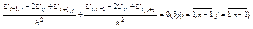(n-1)²уравнения.

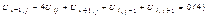Для решения полученой системы уравнений более подходящим является итерационный метод, используем метод Зейделя. Выразим из этого уравнения U_i,j через остальные значения соседних точек. 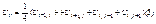. К полученным уравнениям присоединим дискретный аналог граничного условия (2) В это условие производная не входит, поэтому оно заменяется точно через значения функции 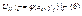Для квадрата можно подробно расписать следующим образом. 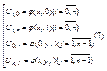определим метод для решения полученной системы уравнений(метод Зейделя). Если проводить вычисления снизу-вверх слева-направо, то формула (5) Может быть записана следующим образом. 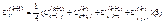к- номер итерации к=0,1,2,3…

Алгоритм реализации.

1) По формуле (7) определим искомое решение на границе области.

2) Зададим начальное приближение. 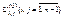Для этого имеются разные способы:

3) Присвоим к=0

4) 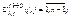по формуле (8)где 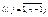найдем новое приближение для искомого решения.

5) Определим максимальное отклонение: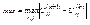

6)если мах>ε(заданной точности), то к=к+1и идти к пункту(4) иначе идти к пункту(7).

7)Вывод полученного решения.