При возрастании количество угловых точек возрастает степень интерполяционного полинома. Полином начинает сильно осцеиллировать, это делает их неудобными для вычисления. Высокой степени можно избежать, если ввести в рассмотрение несколько отрезков. 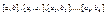 которые в объединение дают отрезок
которые в объединение дают отрезок 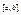
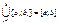 и на каждом из них строить интерполяционный полином, однако в этом случае первая производная терпит разрыв (в точках стыка)
и на каждом из них строить интерполяционный полином, однако в этом случае первая производная терпит разрыв (в точках стыка)
Рисунок
Если узлов n+1, то степень n
Угловые коэффициенты разные 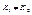 , а значит разные и сами производные в этих точках
, а значит разные и сами производные в этих точках 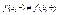 (-слева +справа)
(-слева +справа) 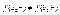 Применение сплайнов избавляет от этого недостатка
Применение сплайнов избавляет от этого недостатка
Опр1. Сплайном (spline-рейка) называется функция, которая на каждом частичном экспериментальном участке представляет собой алгебраический полином (многочлен), а на всем отрезке непрерывна вместе со своими несколькими производными. Существуют сплайны разных степеней на практике наиболее часто используется кубический сплайн.
Кубический сплайн.
Отрезок [a;b] разобьем на n – равных частей точками x; 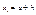 , где
, где 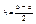
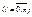
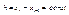 выберем произвольный элемент участок
выберем произвольный элемент участок 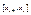
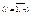 кроме непрерывности самой функции будем требовать непрерывности первой и второй производной
кроме непрерывности самой функции будем требовать непрерывности первой и второй производной
Рисунок
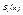 - многочлен, соответствующий участку
- многочлен, соответствующий участку 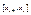
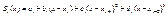 (1) здесь ai, bi, ci, di – пока еще неизвестные коэффициенты (имеем 4n неизвестных коэффициента) Для определения неизвестных коэффициентов будем накладывать условия относительно сплайнов
(1) здесь ai, bi, ci, di – пока еще неизвестные коэффициенты (имеем 4n неизвестных коэффициента) Для определения неизвестных коэффициентов будем накладывать условия относительно сплайнов
Первая группа условий I) потребуем совпадения значения сплайнов и значения функции 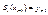 ;
; 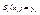
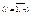 эти условия позволяют нам получить 2n уравнения относительно неизвестных коэффициентов
эти условия позволяют нам получить 2n уравнения относительно неизвестных коэффициентов 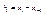 ; подставим уравнение
; подставим уравнение 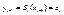
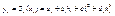
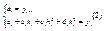 II потребуем непрерывности внутренней узловой точке всего внутри узловых точек(n-1)
II потребуем непрерывности внутренней узловой точке всего внутри узловых точек(n-1) 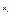
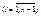 т.е будем накладывать следующего условия
т.е будем накладывать следующего условия 
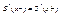 ,
, 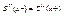 2(n-1) –число, полученное уравнение с помощью следующего условий выражение сплайна для этого участка
2(n-1) –число, полученное уравнение с помощью следующего условий выражение сплайна для этого участка
Рисунок
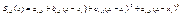 Найдем производные от
Найдем производные от 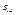 и от
и от 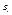 ,
, 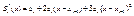 (4)
(4) 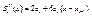 (5)
(5)
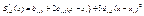 (6)
(6) 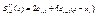 (7)
(7) 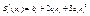 производная справа
производная справа 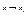 слева производная справа
слева производная справа 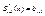 т.о
т.о 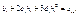 Аналогично, вторые производные Производные слева
Аналогично, вторые производные Производные слева 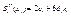 производные справа
производные справа 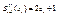 т.о
т.о 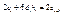 перепишем полученное уравнение
перепишем полученное уравнение 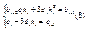
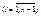 4n-2 –уравнения, а неизвестное 4n.
4n-2 –уравнения, а неизвестное 4n.
Не хватает еще 2х уравнений для получения полностью замкнутой системы. Для получения этих уравнений обычно используют условия на концах отрезках [a;b] т.е 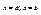 . Можно ставить различные условия для получения недостающих уравнений, обычно используют следующие условие 1) требования нулевой кривизны в точках a и b. Это условие влечет равенство нулю второй производной в точках a и b
. Можно ставить различные условия для получения недостающих уравнений, обычно используют следующие условие 1) требования нулевой кривизны в точках a и b. Это условие влечет равенство нулю второй производной в точках a и b 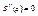
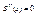 2) первая производная принимает определенное значение в точках a и b
2) первая производная принимает определенное значение в точках a и b 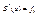
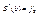 3) вторая производная имеет на концах определенное но не нулевые значения в точках a,b.
3) вторая производная имеет на концах определенное но не нулевые значения в точках a,b. 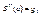
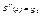 4) условие периодичности т.е в точка a,b сплайн принимает одинаковые значения. Получим дополнительное уравнение на основе первого условия
4) условие периодичности т.е в точка a,b сплайн принимает одинаковые значения. Получим дополнительное уравнение на основе первого условия 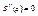
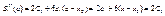 производная справная
производная справная 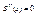
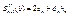 - производная с права
- производная с права 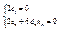 (9)
(9) 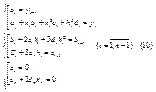 Решая систему уравнения (10) определяют значения неизвестных коэффициентов
Решая систему уравнения (10) определяют значения неизвестных коэффициентов 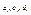 и подставляют эти значения в(1) и получают т.о звенья
и подставляют эти значения в(1) и получают т.о звенья 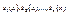 из которых склеивается кубический сплайн на всем отрезке
из которых склеивается кубический сплайн на всем отрезке
Замечание В системе (10) можно сделать преобразования переменных и свести их систему к системе уравнений с трехдиоганальной матрицей. В этом случае для решения системы можно применить метод прогонки.
Теорема. Кубический сплайн построенный на основе рассматриваемых условий существует и является единичным. Матрица системы (10) имеет диагональное преобладание. Это обеспечивает существование единственность решения системы (10) что влечет собой единственность сплайна, определенного на основе формулы (1)
 2015-04-20
2015-04-20 513
513







