2015-04-20
374
Метод Гаусса заключается в последовательном исключении неизвестных. Предположим, что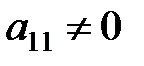 
. В противном случае можно поменять местами первое уравнение с уравнением, в котором коэффициент при 
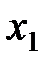не равен 0.
1) Разделим первое уравнение системы на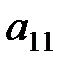 
. Получим
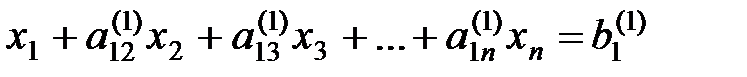, (1.2)
где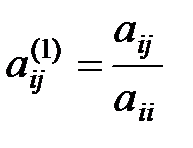 
; 
.
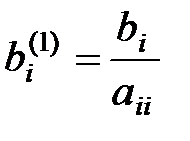2) Умножим разрешающее уравнение (1.2) на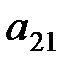 
и вычтем полученное уравнение из второго уравнения системы (1.1). Аналогично преобразуем остальные уравнения:
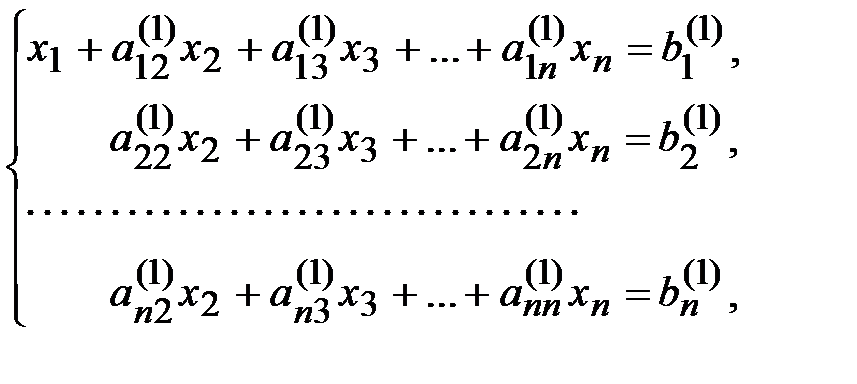(1.3)
где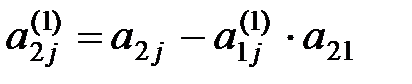 
, 
,…,
, 
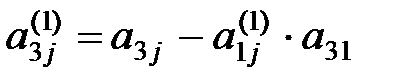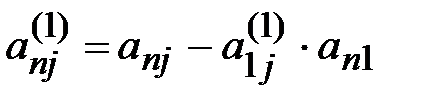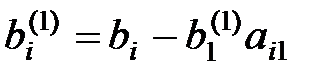(j=2, 3,…, n).
Если коэффициент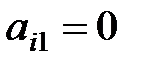 
, то i-е уравнение системы (1.1) войдет в систему (1.3) без изменений, т. е. 
, 
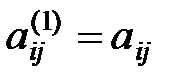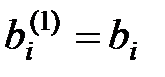, (i = 2, 3,…, n).
3) Оставив без изменений первое уравнение, можно сделать второе уравнение разрешающим и применить описанную процедуру к системе из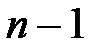 
уравнений, исключив 
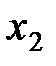из третьего и последующих уравнений
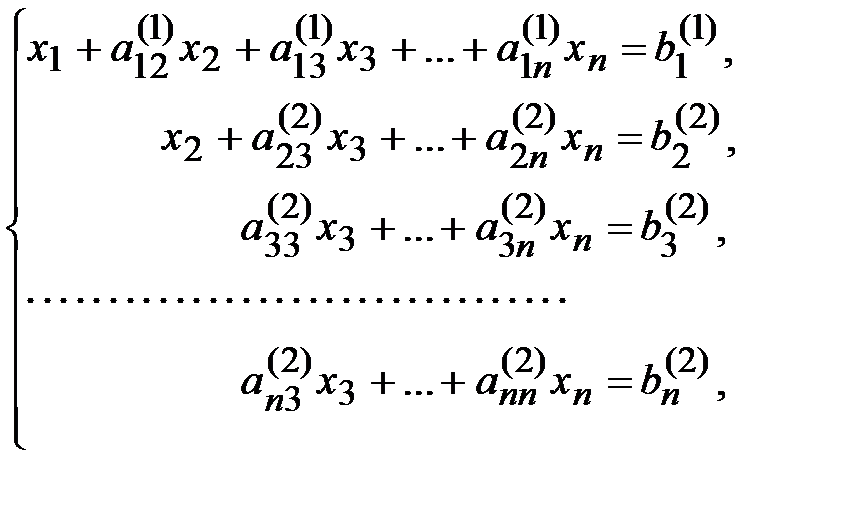
где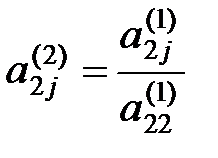 
, 
, 
,…, 
, 
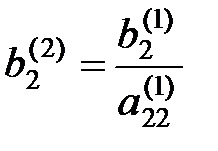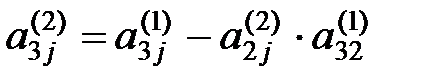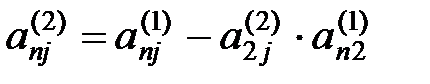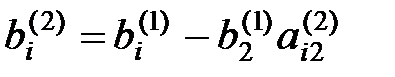(j=3, 4,…, n).
Продолжая аналогичные вычисления, приведем систему (1.1) к эквивалентной системе
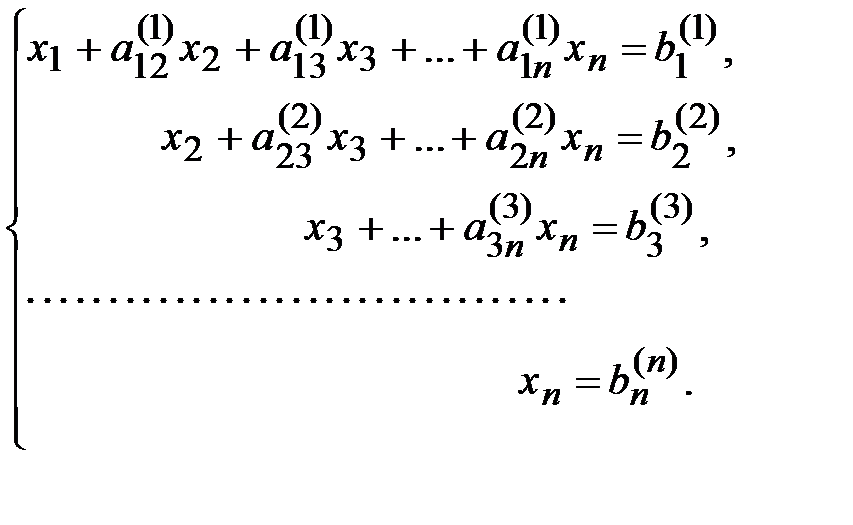(1.4)
Приведение системы (1.1) к эквивалентной системе (1.4) - прямой ход метода Гаусса. При обратном ходе происходит вычисление неизвестных, начиная с последнего, по формуле
|
|
|
.
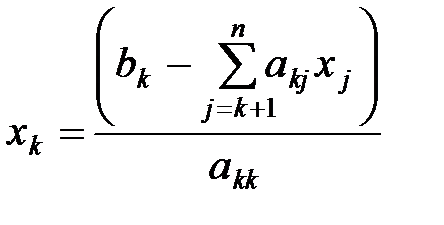Алгоритм данного метода можно записать следующим образом.
1. Для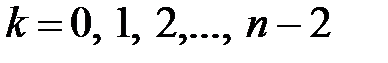 
;
2. для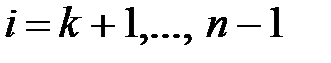 
;
3. 
;
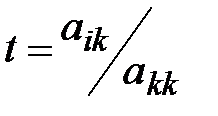4. 
;
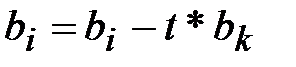5. для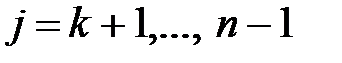 
;
6. 
;
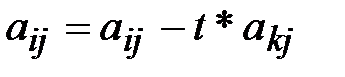7. Для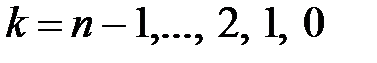 
;
8. 
.
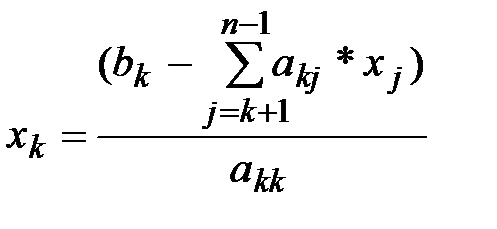Здесь пункты 1 - 6 представляют собой прямой ход, пункты 7 и 8 - обратный ход метода Гаусса.
