2015-04-30
634
В книгах имеются таблицы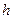 
-функций для единичных трапеций.
Согласно формуле нахождения переходной функции через вещественную частотную характеристику, переходная функция для единичной трапеции имеет следующий вид:
,
,
,
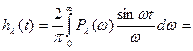
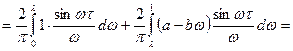
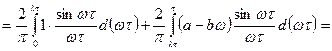
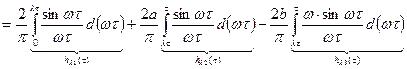
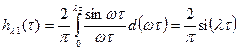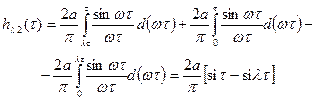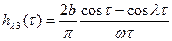где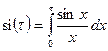 
- интегральный синус.
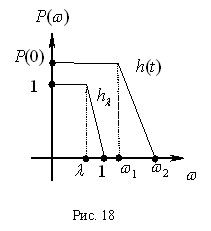
Найдем по графику (рис. 17) значение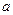 
и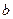 
:
.
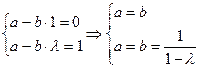Используя соотношения для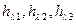 
, 
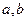, рассчитывается 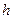-функция для единичной трапеции. Переход от единичной функции к не единичной осуществляется по следующей формуле:
.
.
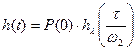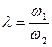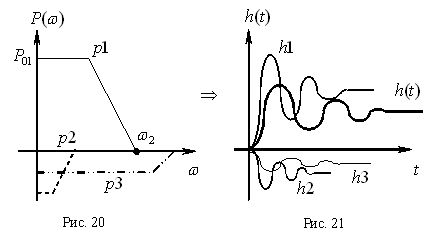
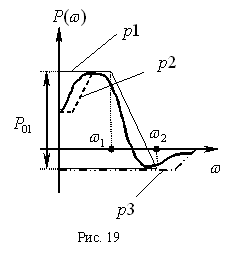Пример: имеем некоторую вещественную частотную характеристику (рис. 19), необходимо получить переходную характеристику. Разобьем исходную характеристику на три трапеций (рис. 20): 
. Для каждой из них получим переходную характеристику, и, сложив их, получим общую переходную функцию (рис. 21).
Переходные характеристики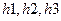 
находятся по таблицам.
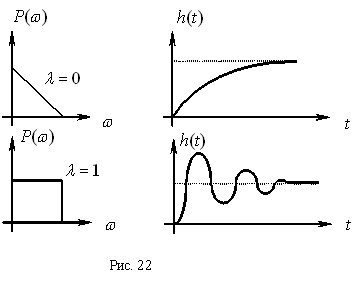
В зависимости от значения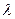 
единичные трапеции могут принимать различные вид. Следует отметить, что чем резче изменяется 
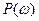, тем более колебательный переходный процесс. Если 
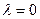, то переходный процесс представляет собой экспоненту, если 
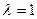, то переходный процесс является колебательным (рис. 22).
|
|
|
