6.2 Основные связи между 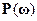 - вещественной частотной функцией и
- вещественной частотной функцией и 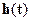 - переходной функцией.
- переходной функцией.
Непосредственно из выражения
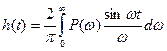 (*)
(*)
вытекают основные свойства 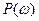 и
и 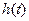 .
.
1. Свойство линейности: если 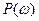 представить в виде суммы
представить в виде суммы
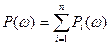 ,
,
Причем
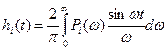 ,
,
то переходная функция 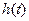 также будет состоять из суммы:
также будет состоять из суммы:
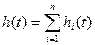 .
.
2. Соответствие масштаба по вертикальной оси: умножив обе части выражение (*) на постоянную 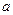 , получаем следующее свойство: при умножении
, получаем следующее свойство: при умножении 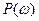 на постоянный множитель
на постоянный множитель 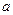 , соответствующие ему значения
, соответствующие ему значения 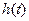 также умножаются на
также умножаются на 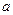 . Иллюстрация данного свойства приведена рис. 15.
. Иллюстрация данного свойства приведена рис. 15.
3. Масштабы по горизонтальной оси обратно пропорциональны (рис. 16): если аргумент 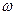 в выражении частотной характеристики умножается на постоянное число
в выражении частотной характеристики умножается на постоянное число 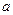 , то аргумент
, то аргумент 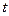 в выражении переходного процесса
в выражении переходного процесса 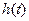 делится на этот множитель:
делится на этот множитель:
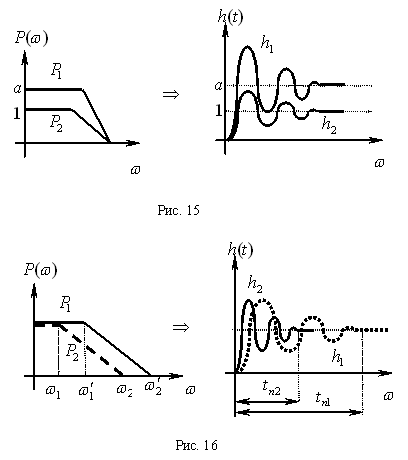
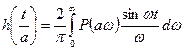 .
.
На рис. 16 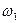 ,
, 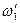 - частоты равномерного пропускания;
- частоты равномерного пропускания; 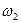 ,
, 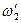 - частоты пропускания,
- частоты пропускания, 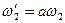 ;
; 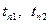 - время переходного процесса.
- время переходного процесса.
Т.о., на сколько увеличилась полоса пропускания, настолько уменьшилась длительность переходного процесса. Чем шире полоса пропускания частот, тем выше быстродействие системы, т.е. короче переходный процесс.
Пример: рассмотрим пропорциональное звено, его передаточная функция имеет следующий вид:
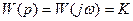 .
.
ЛАЧХ для этого звена представляет собой горизонтальную линию, т.к. полоса частот бесконечна, то переходный процесс происходит мгновенно:
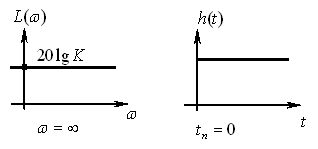
 2015-04-30
2015-04-30 488
488








