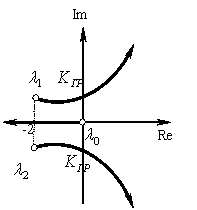
Ветви корневого годографа начинаются в полюсах 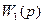 , а заканчиваются в бесконечности.
, а заканчиваются в бесконечности.
Полюса:
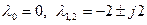 .
.
Значение 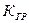 , соответствующее переходу корней из левой полуплоскости в правую, можно подсчитать с помощью критерия Гурвица, или с помощью уравнения фаз.
, соответствующее переходу корней из левой полуплоскости в правую, можно подсчитать с помощью критерия Гурвица, или с помощью уравнения фаз.
Характеристическое уравнение замкнутой системы:
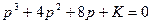 ,
,
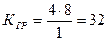 .
.
2. Разомкнутая система имеет следующую передаточную функцию:
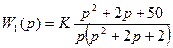 .
.
Нули:
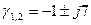 .
.
Полюса:
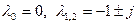 .
.
Характеристическое уравнение имеет следующий вид:
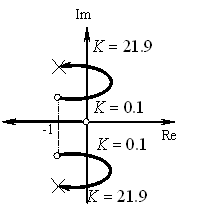
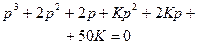 ,
,
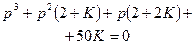 ,
,
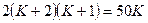 ,
,
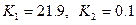 .
.
Система является устойчивой, если 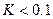 и
и 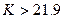 .
.
Система является неустойчивой, если 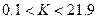 .
.
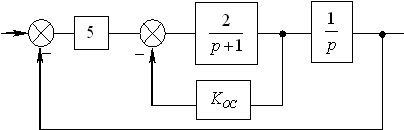
3. Рассмотрим следующую структуру:
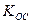 изменяется от
изменяется от 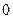 до
до 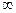 . Необходимо найди те значения
. Необходимо найди те значения 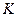 , при которых система имеет максимальное быстродействие.
, при которых система имеет максимальное быстродействие.
Передаточная функция разомкнутой системы имеет следующий вид:
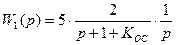 .
.
Характеристическое уравнение:
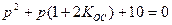 ,
,
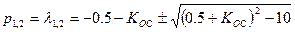 .
.
Если 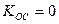 , то
, то 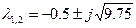 .
.
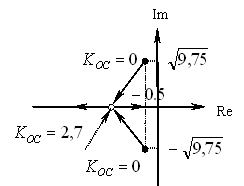 Тогда время переходного процесса определится как:
Тогда время переходного процесса определится как:
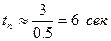 .
.
Т.о. для того чтобы время переходного процесса было минимально, необходимо такое значение 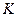 , при котором
, при котором
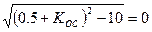 ,
,
 2015-04-30
2015-04-30 347
347








