Замкнутая система имеет следующее характеристическое уравнение:
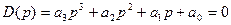 .
.
Чтобы воспользоваться диаграммами Вышнеградского уравнение необходимо записать в форме Вышнеградского, т.е. уравнение необходимо пронормировать:
.
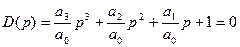 .
.
Вводим новую переменную 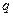 :
:
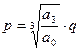 .
.
Получаем уравнение в форме Вышнеградского.:
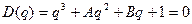 ,
,
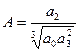 ,
, 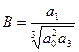 ,
,
где 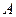 ,
, 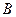 параметры Вышнеградского.
параметры Вышнеградского.
Диаграммы Вышнеградского изобразим в плоскости параметров.
Линия 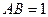 - определяет границу устойчивости системы по Гурвицу (штриховка направлена в область не устойчивости).
- определяет границу устойчивости системы по Гурвицу (штриховка направлена в область не устойчивости).
Если 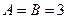 , то
, то
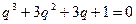 ,
,
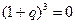 ,
,
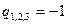 ,
,
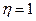 .
.
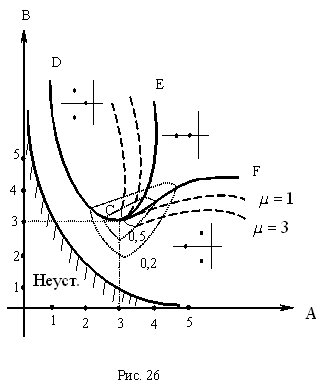
В области CEF все корни – вещественные отрицательные. В области CAF – ближайший корень комплексно-сопряженный, остальные вещественные отрицательные. В области DCE - ближайший корень вещественный, остальные комплексно-сопряженные.
На диаграмме Вышнеградского (рис. 26) обычно показаны линии одинаковой степени устойчивости (изображены пунктиром) и линии одинаковой колебательность (изображены прерывистой линиями). Наибольшая степень устойчивости в точке С.
8. 4 корневой годограф: построение корневого годографа и примеры корневого годографа.
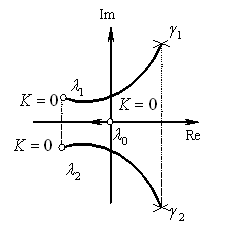
Корневой годограф - траектории корней характеристического уравнения замкнутой системы при изменении одного из параметров системы (обычно статического коэффициента передачи) от 0 до  .
.
Разомкнутая система описывается следующей передаточной функцией:
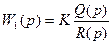 .
.
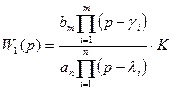 ,
,
где 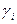 - нули системы,
- нули системы, 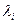 - полюса системы.
- полюса системы.
Тогда замкнутая система имеет следующую передаточную функцию:
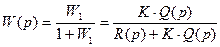 .
.
Характеристическое уравнение замкнутой структуры:
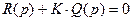 , где
, где 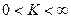 .
.
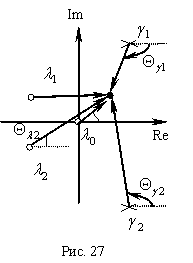
При 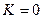 и
и 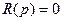 , т.е. годограф начинается в точках, соответствующих корням полинома
, т.е. годограф начинается в точках, соответствующих корням полинома 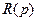 - полюсам
- полюсам 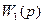 .
.
Пусть полином 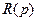 имеет степень
имеет степень 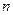 , а полином
, а полином 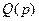 степень
степень 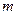 :
:
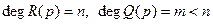
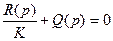 ,
,
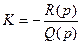 ,
,
если 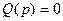 , то
, то 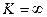 .
.
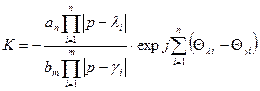 , (*)
, (*)
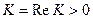 .
.
Из выражения (*) получим уравнение модулей:
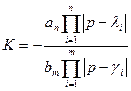
и уравнение фаз:
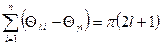 , где
, где 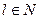 .
.
В каждой точке годографа должно выполняться уравнение фаз (рис. 27):
 2015-04-30
2015-04-30 1197
1197








