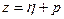 . (*)
. (*)
Увеличивая 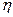 , как бы отодвигаем влево мнимую ось Im на величину
, как бы отодвигаем влево мнимую ось Im на величину 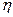 . При некотором значении
. При некотором значении 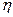 , система в новой переменной
, система в новой переменной 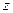 теряет устойчивость. Это означает, что мнимая ось натыкается на ближайший к мнимой оси корень системы, что позволяет определить степень устойчивости исходной системы.
теряет устойчивость. Это означает, что мнимая ось натыкается на ближайший к мнимой оси корень системы, что позволяет определить степень устойчивости исходной системы.
Из выражения (*) получим следующее:
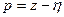 .
.
Подставим последнее соотношение в исходное характеристическое уравнение:
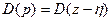
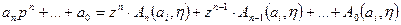 ,
,
где 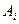 - некоторые функции, зависящие от коэффициентов характеристического уравнения
- некоторые функции, зависящие от коэффициентов характеристического уравнения 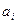 и
и 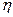 .
.
Составим матрицу Гурвица:
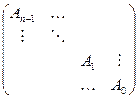 .
.
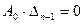 , (**)
, (**)
где 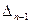 - (
- (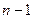 ) – диагональный минор матрицы.
) – диагональный минор матрицы.
Соотношение (**) может выполняться в двух случаях, если 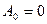 или
или 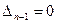 .
.
1) Если первым обращается в ноль 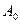 , то это означает, что есть корень
, то это означает, что есть корень 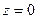 , откуда получим, что
, откуда получим, что 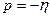 . Т.е. ближайшим к мнимой оси будет вещественный отрицательный корень.
. Т.е. ближайшим к мнимой оси будет вещественный отрицательный корень.
2) Если первым обращается в ноль 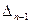 , то ближайшим к мнимой оси будет комплексно-сопряженный корень.
, то ближайшим к мнимой оси будет комплексно-сопряженный корень.
Функции 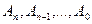 можно найти, разложив полином
можно найти, разложив полином 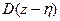 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 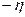 .
.
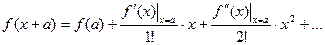
Пример: задано следующее характеристическое уравнение
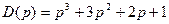 ,
,
необходимо найти степень устойчивости системы 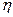 .
.
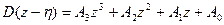 ,
,
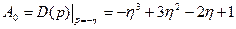 ,
,
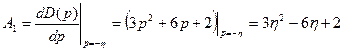 ,
,
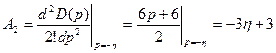 ,
,
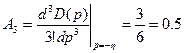 .
.
Составим матрицу Гурвица:
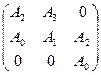 ,
,
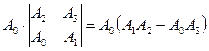 .
.
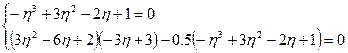 .
.
Из последней системы найдем значение 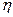 (вещественные положительные значения):
(вещественные положительные значения):
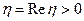 .
.
Применение смещенного уравнения целесообразно применять в системах высокого порядка. Если основное влияние на переходный процесс оказывает только ближайший к мнимой оси корень и он некратный, то длительность переходного процесса определяется следующим образом:
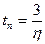 ,
, 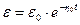 .
.
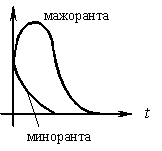
График для минимального переходного процесса называется минорантой.
Наиболее длительный переходный процесс получается, если на него оказывает влияние ближайший к мнимой оси корень, и он кратный:
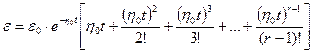 ,
,
где 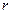 - кратность корня.
- кратность корня.
График для максимального переходного процесса называется мажорантой.
 2015-04-30
2015-04-30 967
967








