Чистое кручение

Как отмечено в разделе 3.2, в этом случае не равно нулю единственное внутреннее усилие – крутящий момент M_k (M_x). Данная ситуация возможна при следующих условиях:

- брус прямой;

- пары внешних сил приложены в плоскостях нормальных к оси бруса, а их векторы направлены вдоль продольной оси OX.

Для того, чтобы выполнялась гипотеза плоских сечений, необходимо чтобы поперечное сечение бруса имело форму круга или кругового кольца (круглый брус). Поэтому ограничимся стержнями удовлетворяющими перечисленным требованиям, а практический расчёт брусьев с иной формой поперечного сечения основанный на известных решениях теории упругости рассмотрим в Приложении.

Отметим, что брус, работающий на чистое кручение или несущий в составе сложной нагрузки значительную составляющую кручения, называют валом.

На рис.6.2а изображен прямой брус с нагрузкой удовлетворяющей указанному требованию.

Рис. 6.2 а – нагружение бруса при чистом кручении; б – эпюра крутящих моментов.

Статическая сторона задачи.

В поперечном сечении бруса с координатой x действует крутящий момент, определяемый методом сечений:

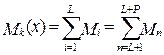, (6.9)

где M_i (i = 1, 2…L) – внешние пары сил приложенные слева от сечения,

M_k (n = 1, 2…P) – внешние пары сил приложенные справа.

Таким образом, крутящий момент равен сумме всех внешних моментов действующих по одну сторону от рассматриваемого сечения, причём пары сил направленные по часовой стрелке (смотреть с торца оставшейся части) берутся со знаком плюс, а направленные против - со знаком минус.

Следуя приведенному правилу, знак крутящего момента в данном сечении получаем автоматически. Если смотреть на оставшуюся часть бруса со стороны сечения, то положительный крутящий момент будет направлен по часовой стрелке (он заменяет действие отброшенной части). На рис.6.2б изображен график изменения крутящего момента вдоль длины бруса, т.е. эпюра M_k(x). При нагружении сосредоточенными парами сил эпюра кутящих моментов имеет вид ступенчатой прямой.

Строго говоря, внешние моменты всегда распределены по какому - то закону m_k(x)=d M_k /dx на участке конечной длины. Величина m_k(x) называется интенсивность распределённого внешнего момента. Если этот участок относительно короткий (например, моменты сил трения в подшипнике скольжения), т.е. занимает менее приблизительно пятой части длины вала, а характер распределения в данной задаче не существенен или не изучен, то, как правило, абстрагируют к сосредоточенному моменту. В других случаях (бур с коронкой) необходимо хотя бы приближенно учитывать этот закон (в коронке момент сосредоточенный, вдоль трубы - распределённый, с интенсивностью, которую в первом приближении можно принять пропорциональной горному давлению).

Основное назначение эпюры M_k– нахождение опасного сечения. Кроме того она является необходимым элементом широко применяемых при вычислениях вручную так называемых графо - аналитических методов.

С другой стороны, крутящий момент является главным моментом касательных напряжений действующих в рассматриваемом сечении:

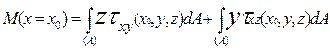(6.10)

Из (5.10) вытекает статическая неопределимость задачи: функции τ_xy(x₀,y,z) и τ_xz (x₀,y,z) неоднозначно определены левой частью этого выражения.

Геометрическая сторона задачи.

Рассмотрим два смежных поперечных сечения круглого бруса (рис.6.3а), с координатами x и x+dx.

Рис. 6.3 Деформации участка круглого бруса при чистом кручении эластичной модели круглого бруса.

После нагружения эти сечения получат угловые перемещения соответственно φ и φ +d φ, оставаясь в соответствии с гипотезой плоских сечений, плоскими и нормальными к оси бруса.

В процессе деформирования ось бруса останется прямой, а перемещения точек такими, что образующая внешней поверхности прямая до нагружения после нагружения закрутится в винтовую линию. Также закрутятся и образующие на поверхности любого внутреннего концентрического слоя материала. Кручение эластичной модели круглого бруса представлено на рисунке 6.3.

Ещё раз подчёркиваем, что указанные рассуждения применимы только к брусу с поперечным сечением в виде круга или кругового кольца. В противном случае поперечное сечение будет депланировать, т.е. получать перемещения из плоскости, что можно наблюдать у эластичной модели в форме прямоугольного параллелепипеда (рис.6.4).

Рис. 6.4 Чистое кручение эластичной модели призматического бруса.

Учитывая вышесказанное, рассмотрим деформации внутренней концентрической поверхности радиуса 0<ρ<R (рис.6.5) элемента бруса длиной dx (рис.5.3а). Здесь R радиус его наружной поверхности.

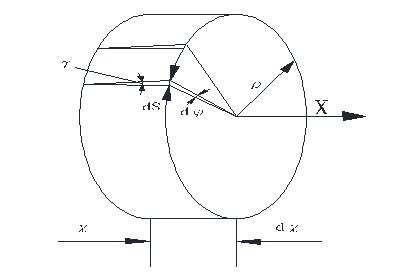
Рис. 6.5 Перемещения в концентрическом слое материала радиуса ρ элемента dx.

Ввиду малости приращения угла закручивания d φ абсолютный сдвиг стороны cd прямоугольного элемента abcd cc₁= ρ dφ Угол сдвига

γ= ρ d φ/ dx (6.11)

Таким образом, рассмотрев кинематику перемещений, мы получили геометрическое условие (6.11), связывающее угол закручивания поперечных сечений бруса φ(x) с угловыми деформациями γ(ρ,φ, x) в концентрических слоях материала.

Физическая сторона задачи.

Из рис.6.5 следует, что при чистом кручении круглого бруса материал концентрических слоёв работает на чистый сдвиг и возникающие касательные напряжения τ связаны с угловыми деформациями γ зависимостью (5.5) – законом Гука при чистом сдвиге.

Обобщение результатов анализа задачи (синтез).

Из рис.6.5 следует, что полные касательные напряжения τ в поперечных сечениях бруса направлены по нормалям к радиус векторам точек, в которых они приложены. Это позволяет упростить условие статики (5.10), т.е. привести его к виду:

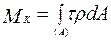(6.12)

Подставив (6.11) в (6.5) получим

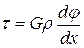(6.13)

Подставляя (6.13) в (6.12) найдём

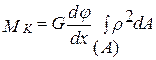
или 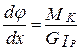, (6.14)

где произведение GI_P называется жесткость бруса на кручение, а интеграл 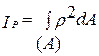, (6.15)

зависящий только от размеров и формы сечения - полярным моментом инерции площади поперечного сечения бруса.

Т.к. в данном случае практический интерес представляют только круглое и кольцевое поперечные сечения, то для круга диаметром D получим

I_P=πD⁴/32, (6.16)

для кольца с внутренним диаметром d

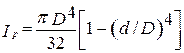. (6.17)

Вывод этих формул предлагается выполнить самостоятельно.

Обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными (6.13) носит название дифференциальное уравнение кручения бруса. Проинтегрировав обе части этого уравнения от x=a до x, получим

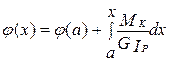. (6.18)

Если на участке a< x< b M_K / GI_P = const, то сечение x=b закрутится относительно сечения x=a

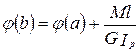, (6.19)

где l=b-a.

Для ступенчатого бруса имеющего n участков жесткостью GI_i=const идлиной l_i , каждый из которых нагружен крутящим моментом M_i=const получим угол закручивания конца k -го участка (k ≤ n) относительно начала

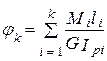(6.20)

Сравнивая далее (6.14) и (6.13) получим

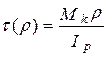(6.21)

- закон распределения полных касательных напряжений по сечению при чистом кручении круглого бруса (формула касательных напряжений при кручении). Из (6.21) следует, что закон этот линейный и касательные напряжения в каждом концентрическом слое материала одинаковы.

На рис.6.6 изображены эпюры τ(ρ) для круглого и кольцевого сечений

Рис.6.6 Чистое кручение. Эпюры касательных напряженной при круглом и кольцевом сечениях.

Видно, что у сплошного сечения материал в центральной части сечения недогружен. Трубчатые валы менее материалоёмки.

Т.к. чистое кручение круглого бруса является комбинацией чистых сдвигов, условие прочности при кручении имеет тот же вид, что и при сдвиге

τ_max ≤ [τ] (6.22)

На основании (6.22) максимальные касательные напряжения можно представить в виде

τ_max=M_k /W _p, (6.23)

где W_p=I_p /R (6.24)

– т.н. полярный момент сопротивления кручению.

Соответственно для круга

W_P=πD³/16, (6.25)

Для кольца 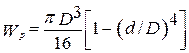. (6.26)

Условие прочности принимает вид

τ_max = M_k /W_p ≤ [τ], (6.27)

откуда с учётом (6.26)

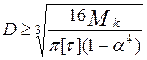, где α = d/D. (5.28)

Примеры решения задач о кручении круглых валов даны в Приложении.

Контрольные вопросы к лекции 6.

1 Что такое чистый сдвиг?

2 Как должен быть загружен элемент материала нормальными напряжениями, чтобы реализовался чистый сдвиг?

3 Что такое площадки чистого сдвига?

4 Как соотносятся величины главных и экстремальных касательных напряжений при чистом сдвиге?

5 Как ориентированы площадки сдвига по отношению к главным?

6 Сформулируйте закон парности касательных напряжений.

7 Что такое абсолютный сдвиг?

8 Что такое относительный сдвиг?

9 Что такое угол сдвига?

10 Связь относительного сдвига и угла сдвига.

11 Что такое модуль сдвига?

12 Закон Гука при сдвиге.

13 Какие механические константы определяют свойства изотропного материала при малых деформациях?

14 Запишите формулу связывающую механические константы изотропного материала.

15 Условие прочности при чистом сдвиге.

16 Что такое допускаемые касательные напряжения?

17 Что такое предельные касательные напряжения?

18 Что такое коэффициент запаса?

19 Чем обусловлен коэффициент запаса?

20 Как связаны допускаемые и предельные напряжения?

21 Какая деформация называется чистым кручением?

22 Какие внутренние усилия возникают в сечениях бруса при чистом кручении?

23 Какие условия должны выполняться, чтобы реализовалась деформация чистого кручения?

24 В каком случае брус называют валом?

25 Всегда ли при кручении цилиндров и призм выполняется гипотеза плоских сечений?

26 Что такое депланация поперечного сечения?

27 В каких случаях для исследования чистого кручения применимы подходы сопромата?

28 Что такое крутящий момент?

29 Как определить крутящий момент в поперечном сечении бруса?

30 Как крутящий момент выражается через напряжения?

31 В чём заключается статическая неопределимость задачи о чистом кручении бруса?

32 Какую деформацию испытывают при кручении концентрические слои круглого бруса?

33 Как деформируется образующая кругового цилиндра при кручении?

34 Выведите зависимость связывающую угловую деформацию γ концентрического слоя радиуса ρ с погонным углом закручивания элемента dx.

35 Запишите дифференциальное уравнение кручения бруса.

36 Что такое полярный момент инерции площади поперечного сечения?

37 Интегрируя дифференциальное уравнение кручения бруса найдите угол взаимного поворота концевых сечений участка длиной l при

M=const, GI_p=const.

38 Чему равен полярный момент инерции площади круга? Докажите эту формулу.

39 Чему равен полярный момент инерции площади кругового кольца? Докажите эту формулу.

40 Чему равен полярный момент сопротивления круга? Приведите доказательство.

41 Чему равен полярный момент сопротивления кругового кольца? Докажите.

42 Запишите формулу касательных напряжений при кручении круглого бруса.

43 Как распределены касательные напряжения по сечению круглого вала при чистом кручении?

44 Изобразите эпюру касательных напряжений в сечении круглого вала при чистом кручении.

45 Изобразите эпюру касательных напряжений в кольцевом сечении вала при чистом кручении.

46 С какой целью применяют валы трубчатой конструкции?

47 Что ограничивает уменьшение толщины стенок трубчатых валов?