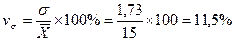2015-04-30
4403
Пример 1. По имеющимся данным узла связи рассчитайте абсолютные и относительные показатели вариации. Сделать вывод об однородности рассматриваемой совокупности и надёжности её средней.
| Количество слов в телеграмме (Хi) | Число телеграмм (fi) |
| Итого |
Решение:
Исходные данные представлены в виде дискретного ряда распределения.
Для исчисления среднего значения признака и показателей вариации строим и рассчитываем вспомогательную таблицу:
| Количество слов в телеграмме (Хi) | Число телеграмм (fi) |  |  |  |  |  |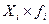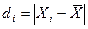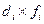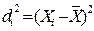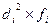
 | ||||||
 | ||||||
 | ||||||
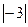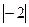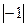| итого |
1). Определяем среднее количество слов в телеграмме по формуле средней арифметической взвешенной, так как исходные данные сгруппированы:
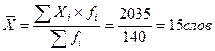
2). Определяем абсолютные показатели вариации:
Размах вариации R=Хmax - Xmin=18-12=6 слов
Среднее линейное отклонение по формуле для взвешенных данных:
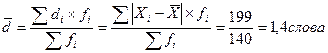
где 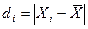- индивидуальное линейное отклонение.
Дисперсию исчисляем по формуле для взвешеных данных
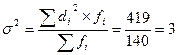
Среднее квадратическое отклонение:
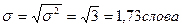
3).Определяем относительные показатели вариации:
Коэффициент осцилляции: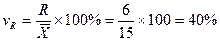 
т.е. колеблемость крайних значений признака вокруг средней составляет 40%.
Линейный коэффициент вариации: 
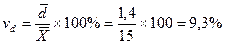, т.е. доля усреднённого значения абсолютных отклонений от средней величины составляет 9,3%.
Вывод: Величина рассчитанного нами коэффициента вариации свидетельствует о том, что колеблемость индивидуальных значений слов в телеграмме невысокая, т.е. Vσ ≤ 33%.
Поэтому совокупность можно считать однородной, а её среднюю – надёжной.
Пример 2. Имеются следующие данные о распределении сотрудников организации по среднемесячной заработной плате. Рассчитать абсолютные и относительные показатели вариации. Сделать вывод об однородности рассматриваемой совокупности и надёжности её средней.
| Группы сотрудников по среднемесячной заработной плате, тыс. руб. | Количество сотрудников, чел. (fi) |
| До 3 3-4 4-5 5-6 6-7 7-8 8-9 9-10 10 и свыше | |
| Итого: |
Решение:
Исходные данные представлены в виде интервального ряда распределения.
Для исчисления среднего значения признака и показателей вариации строим и рассчитываем вспомогательную таблицу:
| Группы сотрудников по среднемесяч- ной заработной плате, тыс. руб. | Централь-ное значение признака в интервале (Хс) | Коли- чество сотруд- ников, чел. (fi) |  |  | |  | |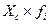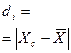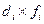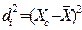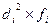
| До 3 | 2,5 | 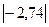 | 38,36 | 7,51 | 105,14 | ||
| 3-4 | 3,5 | 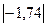 | 38,28 | 3,03 | 66,61 | ||
| 4-5 | 4,5 | 112,5 | 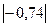 | 18,5 | 0,55 | 13,69 | |
| 5-6 | 5,5 | 159,5 | 0,26 | 7,54 | 0,07 | 1,96 | |
| 6-7 | 6,5 | 1,26 | 12,6 | 1,59 | 15,90 | ||
| 7-8 | 7,5 | 2,26 | 18,08 | 5,11 | 40,86 | ||
| 8-9 | 8,5 | 3,26 | 19,56 | 10,63 | 63,76 | ||
| 9-10 | 9,5 | 47,5 | 4,26 | 21,3 | 18,15 | 90,74 | |
| 10 и выше | 10,5 | 31,5 | 5,26 | 15,78 | 27,67 | 83,00 | |
| итого | 481,66 |
1). Определяем среднюю заработную плату по формуле средней арифметической взвешенной для интервального ряда распределения:
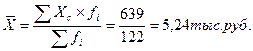
2). Определяем абсолютные показатели вариации:
Размах вариации не рассчитываем, т.к. нижняя граница первого интервала и верхняя граница последнего интервала не указаны.
Среднее линейное отклонение по формуле для взвешенных данных:
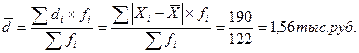
где 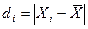- индивидуальное линейное отклонение.
Дисперсию исчисляем по формуле для взвешеных данных:
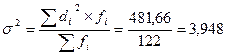
Среднее квадратическое отклонение:
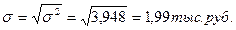
3).Определяем относительные показатели вариации:
Коэффициент осцилляции (VR) не рассчитываем, т.к. не рассчитывали размах вариации.
Линейный коэффициент вариации: 
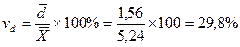, т.е. доля усреднённого значения абсолютных отклонений от средней величины составляет 29,8%.
Коэффициент вариации: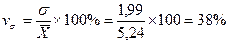 
Вывод: Величина рассчитанного нами коэффициента вариации свидетельствует о том, что колеблемость индивидуальных значений заработной платы высокая, т.е. Vσ ≥ 33%. Поэтому совокупность считаем неоднородной, а её среднюю – ненадёжной.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6.
