С помощью обратной матрицы
Пусть система из n линейных уравнений с n неизвестными записана в матричной форме:
АХ=В,
где А=(aij) – матрица коэффициентов системы размера n ´ n,
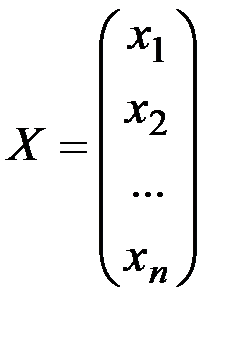 - столбец неизвестных,
- столбец неизвестных,
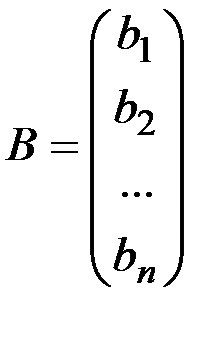 - столбец свободных членов.
- столбец свободных членов.
Если определитель матрицы А не равен нулю, то система совместна и определена, и ее решение задается формулой:
Х=А -1 В.
____________________
1.4.1.Найти матрицу, обратную к данной: а) 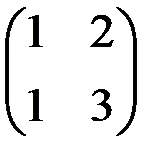 ; б)
; б) 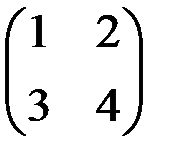 ;
;
в) 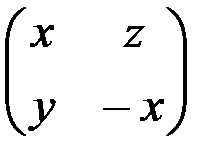 ; г)
; г) 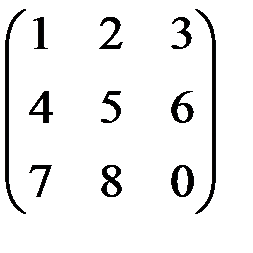 ; д)
; д) 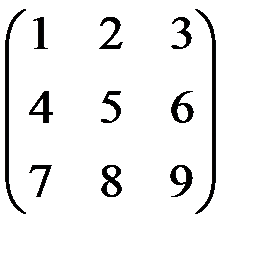 ; е)
; е) 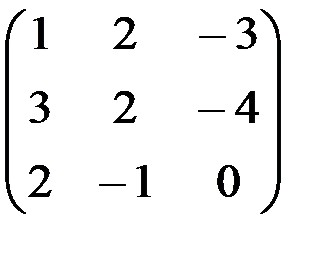 ; ж)
; ж) 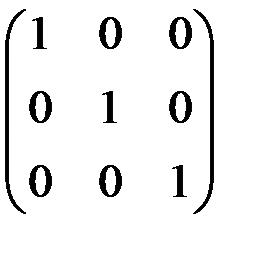 .
.
1.4.2.Решить матричные уравнения: а) 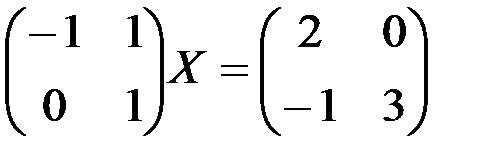 ;
;
б) 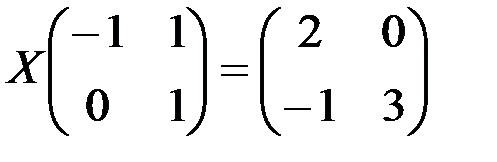 ; в)
; в) 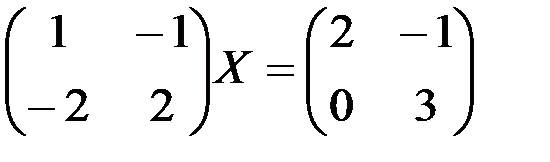 ; г)
; г) 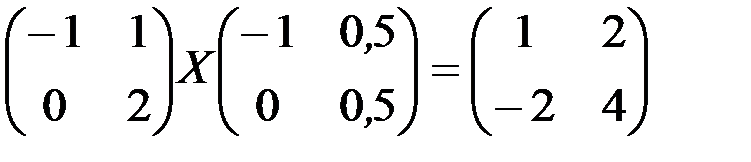 ;
;
д) 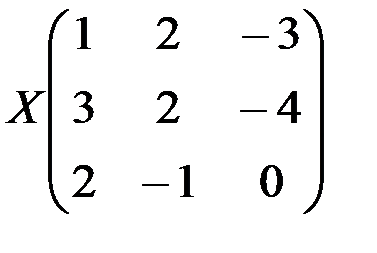
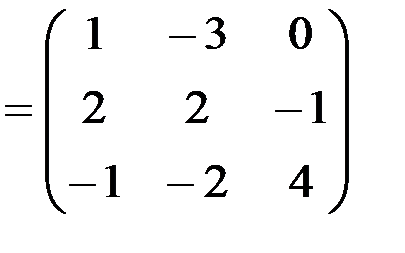 .
.
1.4.3.Решить системы уравнений, используя обратную матрицу: а) 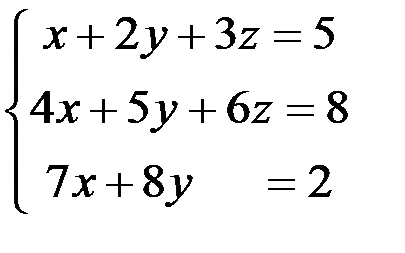 ; б)
; б) 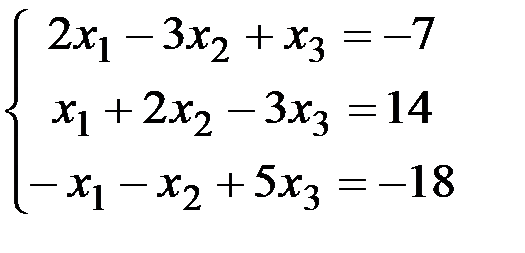 ; в)
; в) 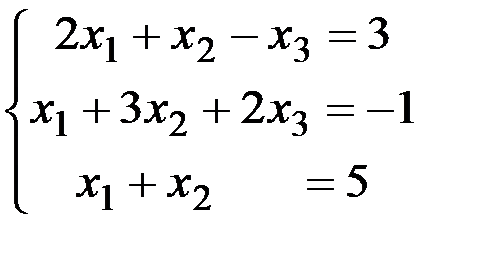 .
.
1.4.4.Решить матричные уравнения:
а) 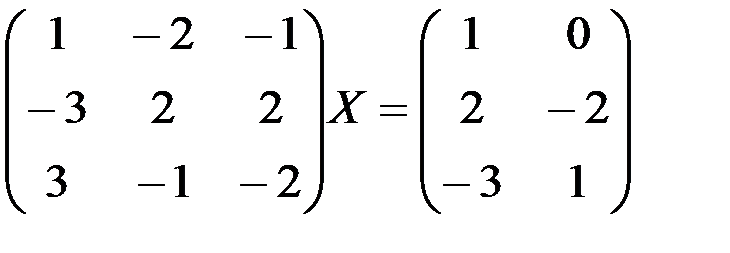 ; б)
; б) 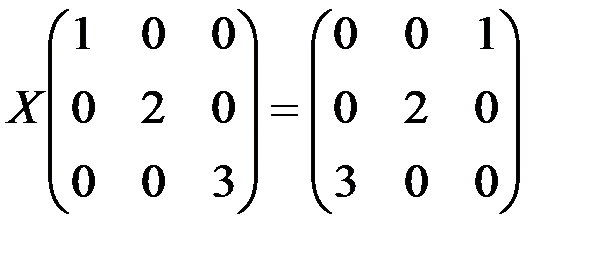 .
.
1.4.5. Решить систему уравнений:
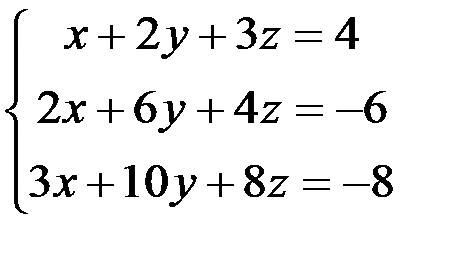 .
.
____________________
Ответы:
1.4.1. а) 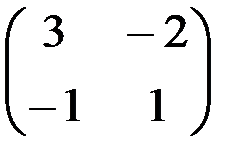 ; б)
; б) 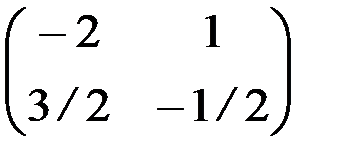 ; в)
; в) 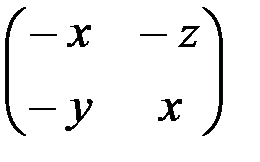 ; г)
; г) 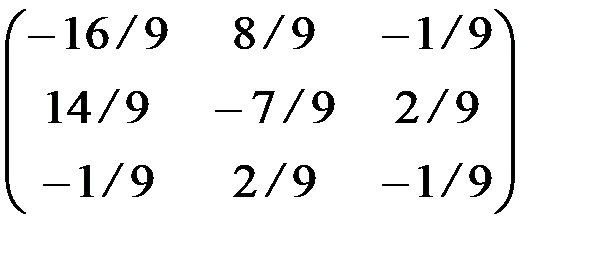 ; д) А -1 – не существует;
; д) А -1 – не существует;
е) 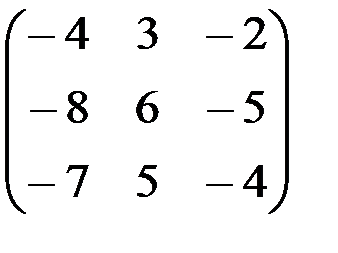 ; ж)
; ж) 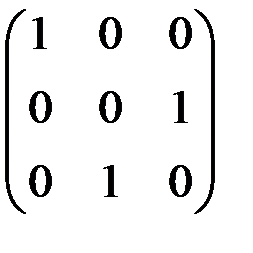 .
.
1.4.2. а) 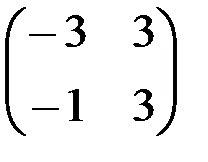 ; б)
; б) 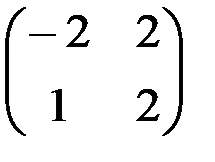 ; в) Х – не существует; г)
; в) Х – не существует; г) 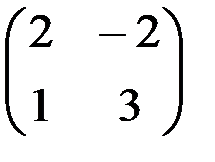 ;
;
д) 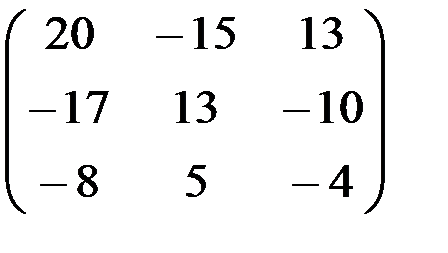 .
.
1.4.3. а) (-2;2;1); б) (1;2;-3); в) невозможно решить.
1.4.4. а) 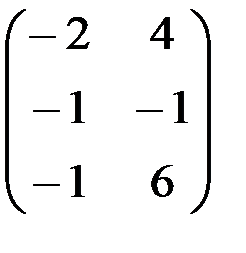 ; б)
; б) 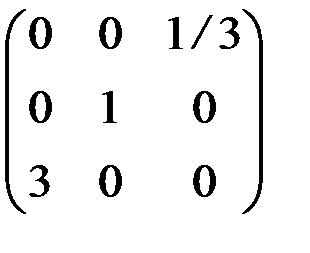 .
.
1.4.5. (2;-3;2).
 2015-04-20
2015-04-20 669
669








