Пусть u=u(x), v=v(x). Тогда
1) (u(x) ± v(x))′=u′(x) ± v′(x);
2) (u(x) v(x))′=u′(x)v(x)+u(x) v′(x);
3) 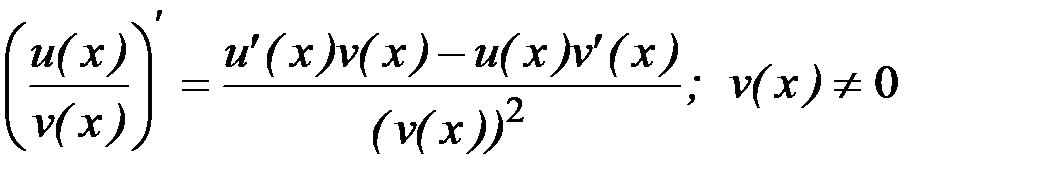 ;
;
4) (cf(x))′= cf ′(x).
Правило дифференцирования сложной функции y=f(u), если u=u(x), состоит (f(u(x))) ′= f′(u)u′(x).
4.3.1. Найти производные следующих функций:
1) f(x)= 3 x 2-5 x +1; 2) 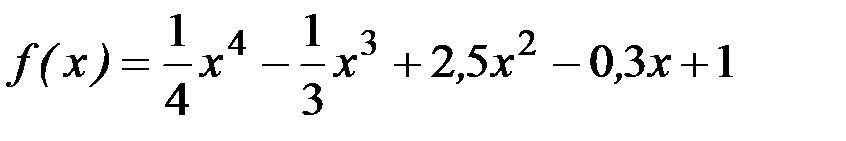 ;
;
3) 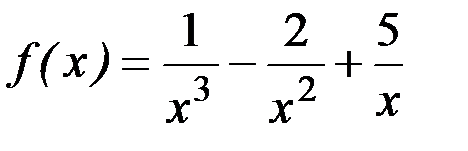 ; 4)
; 4) 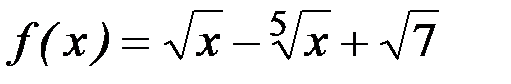 ;
;
5) 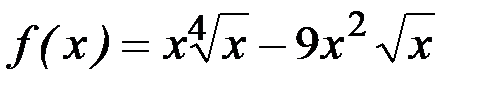 ; 6)
; 6) 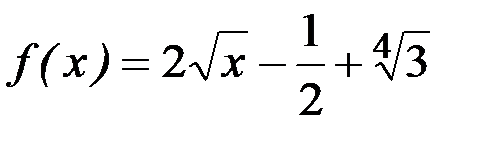 ;
;
7) 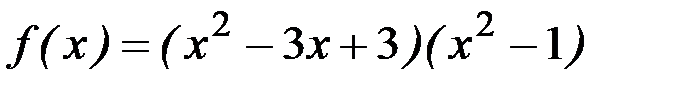 ; 8)
; 8) 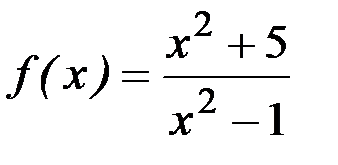 ;
;
9) 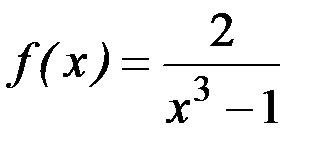 ; 10)
; 10) 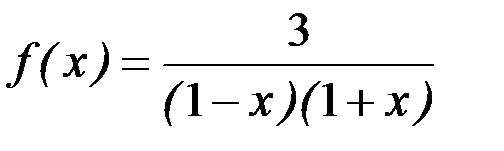 ;
;
11) y=x2sinx; 12) 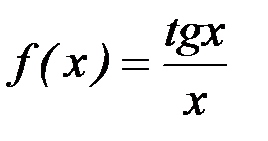 ;
;
13) 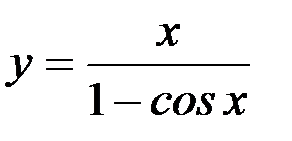 ; 14)
; 14) 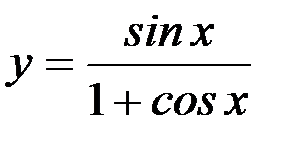 ;
;
15) y=xarcsinx; 16) 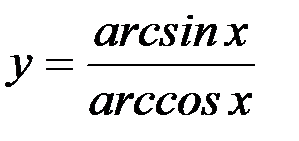 ;
;
17) 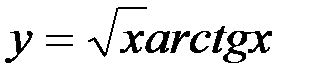 ; 18)
; 18) 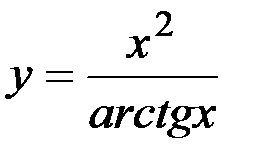 ;
;
19) y=xlnx; 20) 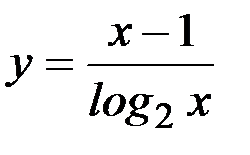 ;
;
21) 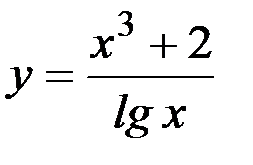 ; 22) y=(sinx)log5x;
; 22) y=(sinx)log5x;
23) y= 2x+10x ; 24) 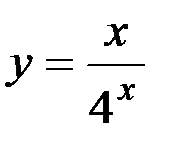 ;
;
25) y=excosx; 26) 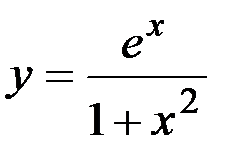 ;
;
27) y=(x 2-10 x +5)10 ; 28) 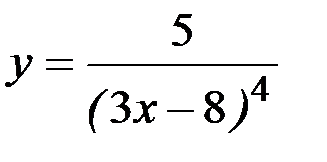 ;
;
29) 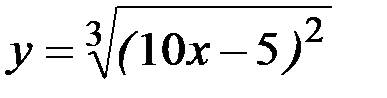 ; 30)
; 30) 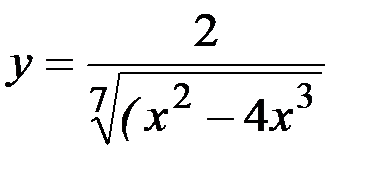 ;
;
31) y=sin 2 x+cos 5 x; 32) y=tgx 2 +ctgx 3 ;
33) y=sin 2 x- 3 cos 3 x; 34) y=tg 35 x;
35) y= 3 sin 2 ( 2 x +5); 36) 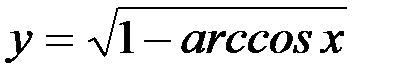 ;
;
37) 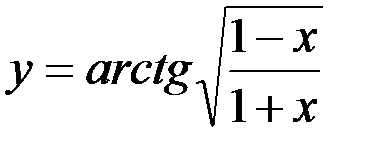 ; 38) y=ln( 1-2 x);
; 38) y=ln( 1-2 x);
39) 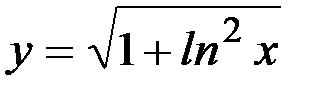 ; 40)
; 40) 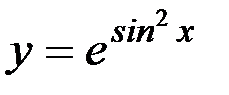 ;
;
41) 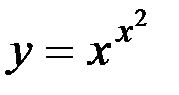 ; 42) y=(sinx)cosx ;
; 42) y=(sinx)cosx ;
43) y=(x+ 5 ) 2/x ; 44) y=(x 2+1 )sinx ;
4.3.2. Найти производные у ′х неявных функций:
1) х 2-5 ху +8 у 3=5; 2) 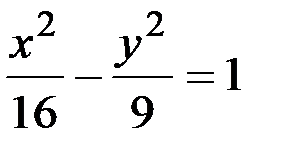 ;
;
3) l 2 x + l 3 y -5 xy =0; 4) lxsiny+lycosx= p;
5) y-x=arctgy; 6) 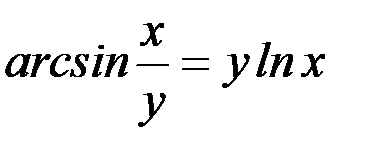 .
.
______________________
4.3.3. Найти производные следующих функций:
1) y=x 4-4 x 3+0,5 x 2-2 x +3; 2) 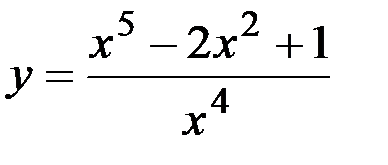 ;
;
3) 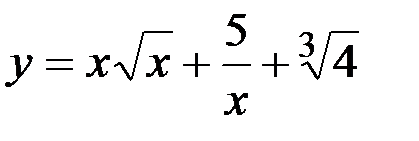 ; 4) y=(x 2+5 x)sinx;
; 4) y=(x 2+5 x)sinx;
5) 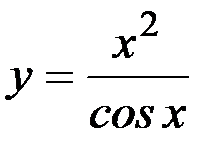 ; 6) y=( 2 x+ 5 ) 7 ;
; 6) y=( 2 x+ 5 ) 7 ;
7) 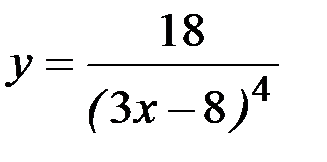 ; 8)
; 8) 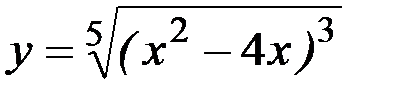 ;
;
9) 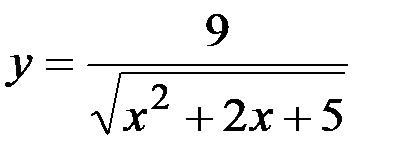 ; 10) y=ln( 5-2 x 2 );
; 10) y=ln( 5-2 x 2 );
11) y=lncos 5 x; 12) 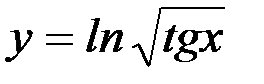 ;
;
13) 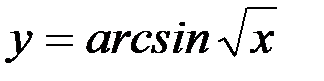 ; 14)
; 14) 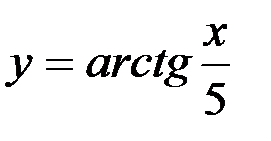 ;
;
15) 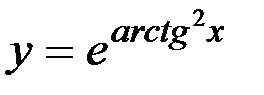 ; 16) y=sin 23 x+sin 9 x 2 ;
; 16) y=sin 23 x+sin 9 x 2 ;
17) 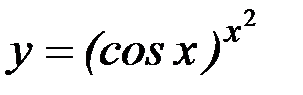 ; 18)
; 18) 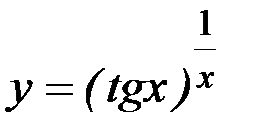 .
.
4.3.4. Найти производные у ′х неявных функций:
1) у 2+ х 2= lnxy; 2) xsiny+ysinx= 0.
 2015-04-20
2015-04-20 559
559








