Первое правило. Неопределенность 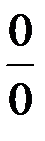 .
.
Если 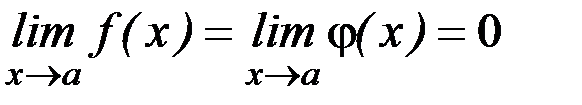 , то
, то 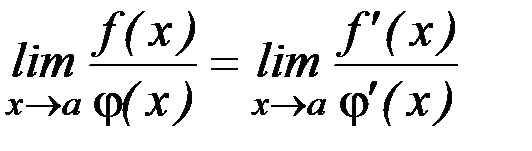 .
.
Второе правило. Неопределенность 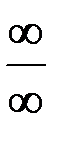 .
.
Если 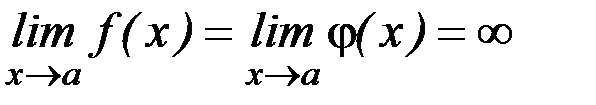 , то
, то 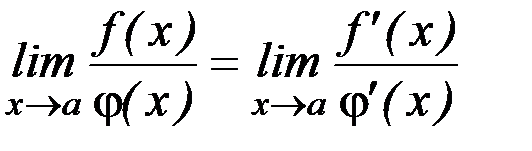 .
.
Неопределенности вида 0∞; ∞-∞; 1∞;00 сводятся к неопределенностям 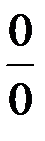 ,
, 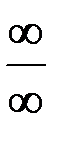 путем алгебраических преобразований.
путем алгебраических преобразований.
______________
4.5.1. Найти производные второго порядка:
а) y=cos 2 x; б) y=arctgx 2 ; в) 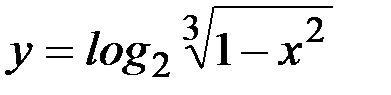 ;
;
г) 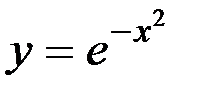 ; д)
; д) 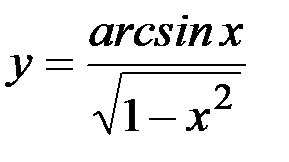 .
.
4.5.2. Найти f' (0), f "(0), f "'(0) если f(x)=e 2x sin 3 x.
4.5.3. Вывести формулу для производной n – го порядка для функций:
а) y=xm; б) у=ах.
Ответ: а) у (n)=m(m- 1 )…(m-n+ 1 )xm-n. б) y(n)=ax(lna)n.
4.5.4. Найти пределы:
а) 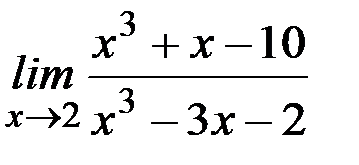 ; б)
; б) 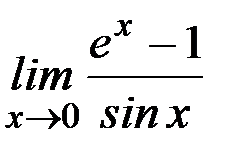 ;
;
в) 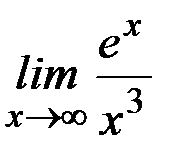 ; г)
; г) 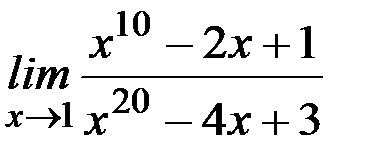 ;
;
д) 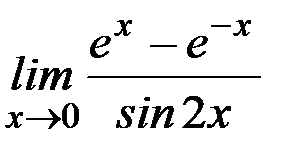 ; е)
; е) 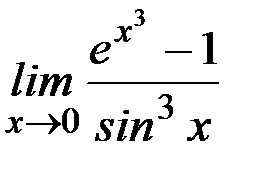 ;
;
ж) 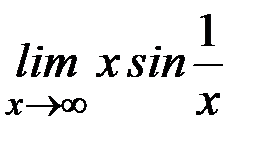 ; з)
; з) 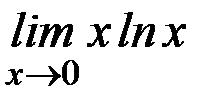 ;
;
и) 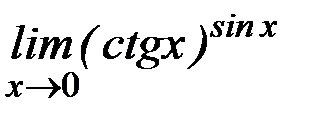 ; к)
; к) 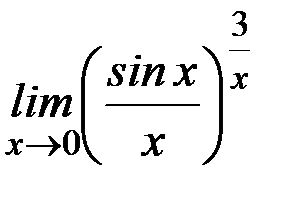 .
.
Ответ: а) 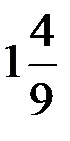 ; б) 1; в) ∞; г) 1/2; д) 1; е)1; ж) 1; з)0; и) 1; к)1.
; б) 1; в) ∞; г) 1/2; д) 1; е)1; ж) 1; з)0; и) 1; к)1.
_________________
4.5.5. Найти производные второго порядка:
а) у=(х 2-10 х +5 ) 5; б) y=sin2x;
в) 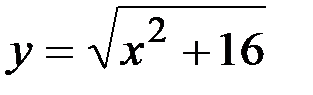 ; г) у=ln(x 3-2 x 2+4).
; г) у=ln(x 3-2 x 2+4).
4.5.6. Найти выражение для n -й производной следующих функций:
а) у =3х; б) у = cosx; в) y=sin 2 x.
4.5.7. Найти пределы:
а) 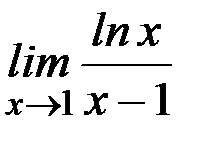 ; б)
; б) 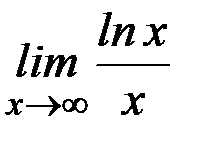 ;
;
в) 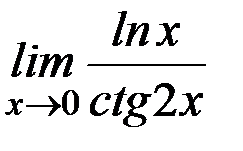 ; г)
; г) 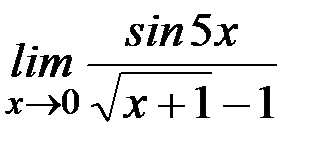 ;
;
д) 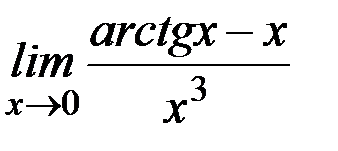 ; е)
; е) 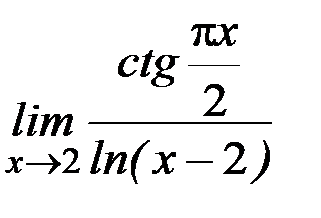 ;
;
ж) 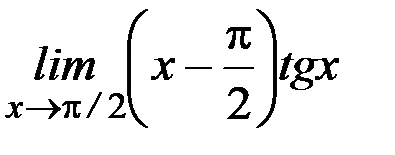 ; з)
; з) 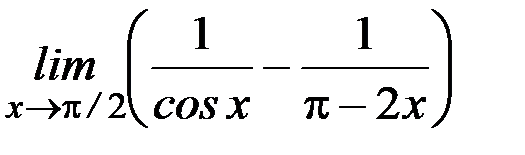 ;
;
и) 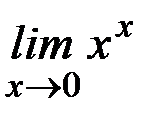 ; к)
; к) 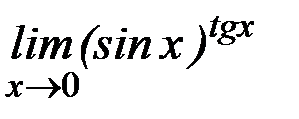 .
.
Ответ: а) 1; б) 0; в)0; г)10; д) -1/3; е)∞; ж) -1; з) 1; и) 1; к)1.
Монотонность функций. Экстремумы.
 2015-04-20
2015-04-20 422
422








